El objetivo fue demostrar que no existe relación entre la tasa de contagio y el movimiento humano. De esta forma, buscando minimizar inicialmente la zona de estudio, se capturaron y analizaron datos extraídos de Ecuador a nivel provincial hasta un estudio más generalizado con respecto a Suramérica, donde cada región de estudio era un país y no una provincia. En este estudio se aplicó una serie de experimentos utilizando modelos de regresión lineal en 3 variantes diferentes, en movimientos tipo 1, tipo 2 y en una variante que utiliza los dos tipos de movimiento, siendo este el que marcó la diferencia en los resultados. Por lo tanto, para mejorar el tiempo de detección de nuevos infectados, se creó un modelo que usando como base un periodo de incubación de 12 días buscase aquellos días posteriores con la mejor correlación posible en los datos.

Descriptores: Epidemiología; infecciones por coronavirus; coronavirus. (Fuente: DeCS2020).

ABSTRACT

The objective was to demonstrate that there is no relationship between the contagion rate and human movement. In this way, initially seeking to minimize the study area, data extracted from Ecuador at the provincial level were captured and analyzed until a more generalized study with respect to South America, where each study region was a country and not a province. In this study, a series of experiments was applied using linear regression models in 3 different variants, in type 1, type 2 movements and in a variant that uses both types of movement, this being the one that made the difference in the results. Therefore, to improve the detection time of new infected, a model was created that, using as a base an incubation period of 12 days, looked for those subsequent days with the best possible correlation in the data.

Descriptors: Epidemiology; coronavirus Infections; coronavirus. (Source: DeCS2020).

INTRODUCCIÓN

En esta era de globalización, los movimientos ininterrumpidos de seres humanos no permiten que ningún país sea inmune a la amenaza potencial de epidemias. Desde 2003, enfermedades contagiosas emergentes como la influenza aviar, Oriente Medio síndrome respiratorio, SARS y Ébola nos recordaron a los seres humanos una vez y nuevamente de la grave amenaza que representan para la salud humana y la seguridad económica y social ⁴.

En diciembre de 2019, un nuevo coronavirus, denominado Síndrome respiratorio agudo severo Coronavirus 2 (SARS-CoV-2) de origen desconocido, se propagó en la provincia de Hubei en China, esta enfermedad epidémica causada por el SARS-CoV-2, es llamada enfermedad de coronavirus-19 (COVID-19). La presencia de COVID-19 se manifestó por varios síntomas, que iban desde pacientes asintomáticos, pasando por síntomas leves hasta enfermedad grave y muerte.

La infección viral se expandió internacionalmente y la Organización Mundial de la Salud (OMS) anunció una Emergencia de Salud Pública de Importancia Internacional, para diagnosticar y controlar rápidamente esta enfermedad tan altamente infecciosa, se aislaron individuos sospechosos y se desarrollaron procedimientos de diagnóstico/tratamiento a través de los datos epidemiológicos y clínicos de los pacientes ^{1 5}.

Sobre la base de los datos de secuenciación y evolución, los murciélagos son el reservorio propuesto para el coronavirus ⁶. Después de su descubrimiento inicial, la propagación del SARSCoV-2 en todo el mundo fue rápida, con más de 1,7 millones de casos confirmados en todo el mundo y más de 100.000 muertes a partir de abril de 2020. La gravedad de esta enfermedad puede variar desde un estado asintomático al síndrome de dificultad respiratoria aguda (SDRA) que requiere medidas agresivas hasta la muerte ⁷.

En América Latina el virus llega tarde, el 25 de febrero de 2020, siendo Brasil el primer país de la región en informar casos positivos de la enfermedad. En unas semanas, los países en todo el continente habían cerrado sus fronteras ⁸. A todo esto, le siguió un rápido crecimiento en el número de casos en toda la región, causando un rápido aumento de casos clínicos de la nueva enfermedad por coronavirus, COVID-19. Varios estudios indicaron que el número reproductivo básico más probable está entre dos y cuatro para el coronavirus (lo que significa que cada individuo infeccioso puede generar directamente entre 2 a 4 personas infectadas) ².

Los gobiernos de cada país están tratando de precautelar la vida de sus habitantes implementando medidas como restricciones de viaje, cuarentenas, aplazamiento y cancelaciones de eventos y el distanciamiento social entre otras. Además de las vidas que ha cobrado este virus, el impacto económico y social es igual de desastroso y especialmente para los países en desarrollo y subdesarrollados ⁹.

Un modelo matemático examinó si el control de la infección por SARS-CoV-2 podría ser logrado aislando a los pacientes afectados y rastreando sus contactos con otros in- dividuos. Este modelo concluyó que aislar a las personas y revisar sus contactos sería insuficiente para controlar la pandemia, porque habría demasiada demora entre el inicio de los síntomas y el aislamiento. Por lo tanto, observar las medidas preventivas especialmente el aislamiento y el encierro, así como evitar lugares públicos abarrotados y mantener al menos dos metros de distancia entre cada persona serían fundamentales ¹⁰.

Hasta ahora existen diversos grupos de investigaciones que han trabajado en este tema en base a diferentes situaciones considerando supuestos tales como variables en base a el ratio de confirmación de nuevos casos positivos con respecto a los números de pruebas realizadas en las regiones ¹⁴, así como valores de vulnerabilidad entre regiones, pe- ro muchas de estas investigaciones están centradas en zonas específicas, lo cual no corresponde a una solución completa sino a un idealismo parcial que pretende, asumiendo dichos valores; hacer un pronóstico de casos del coronavirus sin ser realmente específicos con los resultados y las variantes posibles que puedan existir.

MATERIALES Y MÉTODOS

Se describe a continuación:

Breve descripción de los conjuntos de datos

Para este estudio, se adquirió tres bases de datos diferentes, don- de la información de dos de las bases de datos proviene de la OMS (Organización Mundial de la Salud), la primera base de datos está relacionada con los nuevos casos de coronavirus (incidencia diaria) desde marzo hasta octubre de 2020 en los diferentes países del mundo y la segunda base de datos asociada a los casos positivos de coronavirus desde febrero hasta mayo de 2020 a nivel provincial de países tales como Ecuador, Colombia, Perú, Brasil y Argentina; y la información de la última base de datos está relacionada con la ratio de movimiento que se encuentra dividida por ciudades de cada país.

Definición de los conjuntos de datos

Los datos extraídos de la primera base de datos a nivel mundial proveniente del sitio web HDX ¹², presentan como atributos: fecha de reporte, código del país, nombre del país, región de la OMS, número de nuevos casos, número de casos acumulados, número de nuevas muertes y número de muertes acumuladas.

El segundo dataset, a nivel provincial fue extraído a partir de un conjunto de datos en formato Excel proveniente del sitio web Figshare ¹⁵, en el que se representa por cada hoja un país, y dentro de cada hoja se encuentran las subregiones de cada país, con los datos de la fecha, en las que adjunta a cada subregión: número de casos positivos, número de muertes y número de casos recuperados.

El tercer dataset cuyos datos son proporcionados por Facebook, también provenientes del sitio web HDX ¹², presenta los siguientes atributos: identificador para cada objeto, fecha en la que se extraen los datos, código del país, origen del código de la región (polígono), regiones, número identificador del polígono de la región, movimiento tipo 1 (cambio positivo o negativo en el movimiento con respecto a la línea de base), movimiento tipo 2 (proporción positiva de usuarios que se quedan en una única ubicación), cuándo se calculó el movimiento de la línea de base antes de Covid-19 y cómo se calculó el movimiento de la línea de base antes de Covid-19.

Los polígonos dentro de este último dataset hacen referencia a una cobertura regional especificada en cuartiles a través de fórmulas que buscan cubrir ciertas coberturas de un mapamundi. Estas son llamadas Quadkeys o teselas y su dimensión es de (2)2, conocido también como Mapa de teselas de nivel 16.

Figura 1: Mapa con teselas (quadkeys) de nivel 7.

Base de datos 1	Muestra 1	Muestra 2	Muestra 3
Date reported	2020-03-14	2020-10-03	2020-09-24
Country code	AR	CL	EC
Country	Argentina	Chile	Ecuador
WHO region	AMRO	AMRO	AMRO
New cases	14	1840	2339
Cumulative cases	49	466590	129982
New deaths	1	45	45
Cumulative deaths	2	12867	11171

Tabla 1: Encabezados de la primera base de datos sobre los nuevos casos de coronavirus a nivel mundial.

Base de datos 2

Muestra 1

Unnamed: 0 ds

country polygon source polygon id polygon name

all day bing tiles visited relative change all day ratio single tile users

baseline name

baseline type

1184859

01/03/20

ECU GADM ECU.14.10₁

Manta

-0.19535

0.29915

full_february DAY_OFF_WEFK

Tabla 2: Encabezados de la segunda base de datos sobre el ratio de movimiento a nivel mundial dividido por polígonos.

Base de datos 3	Muestra 1	Muestra 2	Muestra 3
Fecha	19/05/2020	20/05/2020	22/05/2020
Positivo	730	766	782
Muertos	29	30	33
Recuperados	NaN	NaN	NaN
Fecha	19/05/2020	20/05/2020	22/05/2020

Tabla 3: Encabezados de la tercera base de datos sobre casos de coronavirus en ciertos países de Latinoamérica divido por provincias.

Exploración de datos

Para esta investigación se consideró las siguientes premisas:

1. Se precisó usar solamente la información de los casos positivos debido a que los datos de muerte son imprecisos, es decir no son fieles y carecen de representatividad.

2. Para el dataset que representa los datos positivos en este estudio, se decidió que los mejores datos son aquellos que constituyen los nuevos casos diarios, por cuanto estos permiten trabajar un manejo más fiable de predicción.

Dentro del dataset de movimientos se consideró evitar variables como: origen de los polígonos, nombre de la línea de partida y tipo de línea de partida, por cuanto no tienen ninguna representación para su uso en la investigación.

1. Para el dataset de la OMS no se consideraron los da- tos acumulados, región de distribución de la OMS y código de país.

2. El rango de movimiento posee datos que presentan un comportamiento inversamente proporcional, por lo cual su estudio como variables independientes no re- presentan su uso en una regresión múltiple, decidiéndose así utilizar un modelo de regresión lineal.

3. Debido a que el tipo de predicción que se quería lograr no era binario, se evitó escoger la regresión logística.

Preparación de datos

Bajo el uso del lenguaje de programación “Python” y el ambiente en nube “Colaboraty” se realizó los dos juegos de datos en base al movimiento regional de cada uno (relación casos positivos - movimientos). El primero en base a las provincias de Ecuador y el segundo en relación a las regiones suramericanas.

Los juegos de datos mantienen una estructura de datos que durante el transcurso de la investigación fueron denominados como diccionarios, estos diccionarios dividen la data por secciones ya sea por país o por provincias dependiendo del juego de datos denominados como subconjuntos, teniendo así dos diccionarios por cada juego de datos:

4. Contagio: Almacena los datos referentes al aumento diario de nuevos casos de coronavirus por cada subconjunto.

5. Movimiento: Almacena los datos referentes a los movimientos tipo 1 y tipo 2 por día de cada subconjunto.

A continuación, se presentan resúmenes estadísticos de algunos subconjuntos de ambos juegos de datos.

Manabí

			Índice de Contagio
	Conteo Media dte min max		84.00 0.18 0.79 0.00 7.00
		Movimiento 1		Movimiento 2
Conteo Media dte min max		209 -0.36 0.20 -0.74 0.00		209 0.41 0.10 0.22 0.65

Tabla 4 y 5: Resumen estadístico de las variables índice de contagio, Movimiento tipo 1 y Movimiento tipo 2 para la provincia de Manabí.

Ecuador

			Índice de Contagio
	Conteo Media dte min max		264 0.67 3.53 0.00 48.00
		Movimiento 1		Movimiento 2
Conteo Media dte min max		218 0.32 0.19 0.04 0.71		218 0.36 0.10 0.19 0.60

Tabla 6 y 7: Resumen estadístico de las variables índice de contagio, Movimiento tipo 1 y Movimiento tipo 2 para el país de Ecuador.

Modelado

Técnicas de modelado Al necesitar predecir una variable dependiente (Nuevos casos de Coronavirus diarios), a partir de una variable independiente (Ratio de Movimiento diario), donde ninguna de estas es categórica (eliminando la regresión logística como opción), al manejar solo una variable independiente se catalogaría como un problema de regresión lineal simple.

Y_i = β₀ + β₁X_i

Donde:

0. Y representa el valor de predicción (contagio por día).

1. X representa el valor de entrada a predecir (ratio de movimiento por día).

2. β mide la influencia que tiene la variable independiente sobre la variable dependiente.

Métricas de Calidad

De la cantidad total de datos se utilizó el 70 % de los datos para el entrenamiento del modelo y el porcentaje restante se utilizó para el testing (pruebas) del modelo, debido a que es el que mejor resultados proporciona dentro de distintas particiones sin empobrecer los datos de entrenamiento, como lo recomiendan ¹⁶ para evitar el problema de sobre-entrenamiento.

Para la medición de calidad de los resultados se utiliza- ron las siguientes métricas:

Construcción del modelo

Durante el transcurso de la investigación se tuvo que realizar varios cambios al modelo de predicción de forma que el proceso fuese lo más ajustado posible a realizar la predicción (lo que la investigación busca negar), los modelos resultantes cronológicamente fueron los siguientes:

En primer lugar, se usó el conjunto de datos de ratio de movimiento como un valor independiente, intentando predecir el nuevo número de casos por día relacionando el movimiento de un día 0 con los nuevos casos de coronavirus en el día 12, número de días promedio para el periodo de incubación del coronavirus, de esta forma se tiene en cuenta el tiempo en el que los casos nuevos son detectados, en este modelo se utilizó 3 variantes:

– La primera variante utilizaba el movimiento tipo 1.

– La segunda variante utilizaba el movimiento tipo 2.

– La tercera variante utilizaba los dos tipos de movimientos.

Se creó un segundo modelo en el que se usó como dato independiente un índice de aumento de movimiento, es decir, se convirtieron los datos de movimiento en aumentos porcentuales diarios y como valor a predecir el número de casos nuevos de coronavirus siguiendo el mismo esquema de días que el modelo previo.

Finalmente se creó un tercer modelo en el que se usó como dato independiente un índice de aumento de movimiento y como valor a predecir el índice de nuevos casos de coronavirus usando la misma lógica del índice de movimiento, convirtiéndolos a valores porcentajes.

Con este modelo se creó además un proceso de búsqueda para identificar que, días, pasado el período de incubación, presentaban mejor correlación usando el coeficiente de relación de Pearson como herramienta para esta tarea con los datos del movimiento del día cero, de esta forma forzar mayor probabilidad de una predicción exitosa.

Para todos los modelos se probaron variantes donde se restringió, los cálculos de entrenamiento por debajo de la mediana en un intento de eliminar los outliers.

RESULTADOS

Evaluación del modelo

Al utilizar un filtro de datos bajo la mediana del conjunto de datos para probar si la eliminación de los outliers facilitaba la obtención de r2, se concreta que este cálculo no realizó un cambio representativo para los datos.

Para evaluar el modelo

Para probar cada modelo adecuadamente, se tomaron 5 muestras iterando sobre un proceso de entrenamiento y predicción para verificar que tan estable es el modelo este proceso se repitió para 3 subconjuntos, esto con cada modelo para poder realizar las comparaciones correspondientes, buscando que se presenten los menores cambios posibles entre iteraciones. A esto nos referiremos como "análisis de estabilidad predictiva" al evaluar qué tanto cambian sus valores entre muestras.

Tras analizar la información de los modelos de contagio - movimiento mencionados en la sección anterior, en el primer modelo se detectó lo siguiente:

Guayas

Muestra	ECM	R2
1	190753.17	0.05
2	211454.64	0.04
3	20.152.78	0.13
4	213960.21	0.05
5	154400.84	0.05

Tabla 8: Métricas de calidad de muestra en 5 iteraciones diferentes para el primer modelo en la provincia de Guayas.

Manabí

Muestra	ECM	R2
1	4587.67	0.02
2	3705.67	0.01
3	4.100.44	0.02
4	4167.15	0.02
5	4601.17	0.02

Tabla 9: Métricas de calidad de muestra en 5 iteraciones diferentes para el primer modelo en la provincia de Manabí.

Pichincha

Muestra	ECM	R2
1	1864.12	0.11
2	2856.23	0.04
3	3086.92	0.03
4	2651.72	0.04
5	3019.25	0.04

Tabla 10: Métricas de calidad de muestra en 5 iteraciones diferentes para el primer modelo en la provincia de Pichincha.

Se observó un error cuadrático medio elevado. Al estar alejado a 0, implica baja precisión en la predicción. Esto nos indica que es un modelo no funcional y que nunca presentaría una predicción debido al gran número de errores que pueda presentar.

Se presenta una R² muy cercano a 0 en todos los datos, por lo cual el modelo es invariable, en otras palabras, la predicción es imprecisa.

A partir de estos resultados, en el segundo modelo se pensó en crear un valor porcentual para describir los cambios de forma homogénea, obteniendo lo siguiente:

Empeora el modelo previo al mantener un ECM demasiado alto. A demás de esto logra que el coeficiente de determinación permanezca en todo momento bajo el 2% (0.02).

Guayas

Muestra	ECM	R2
1	146697.36	0.01
2	214976.03	0.01
3	148808.17	0.01
4	223700.76	0.01
5	218226.47	0.01

Tabla 11: Métricas de calidad de muestra en 5 iteraciones diferentes para el segundo modelo en la provincia de Guayas.

Manabí

Muestra	ECM	R2
1	218226.47	0.01
2	4556.05	0.00
3	4544.03	0.01
4	4544.03	0.01
5	1571	0.00

Tabla 12: Métricas de calidad de muestra en 5 iteraciones diferentes para el segundo modelo en la provincia de Manabí.

Pichincha

Muestra	ECM	R2
1	3265.47	0.01
2	3067.52	0.02
3	3443.37	0.02
4	3334.27	0.02
5	3293.06	0.00

Tabla 13: métricas de calidad de muestra en 5 iteraciones diferentes para el segundo modelo en la provincia de Pichincha.

Guayas

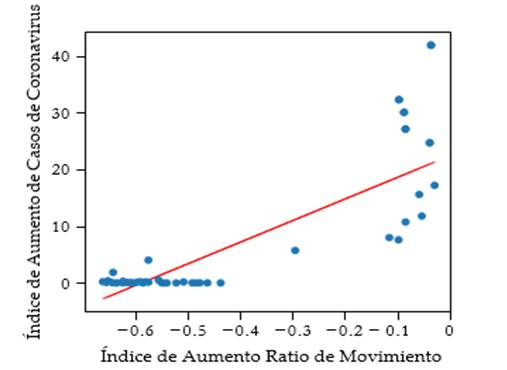
Figura 3. Resultado modelos predictivo contra datos de entrenamiento en Guayas.

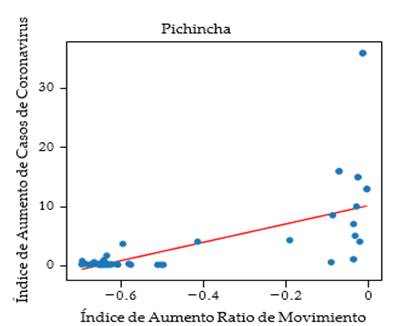
Figura 4. Resultado modelos predictivo contra datos de entrenamiento en Pichincha.

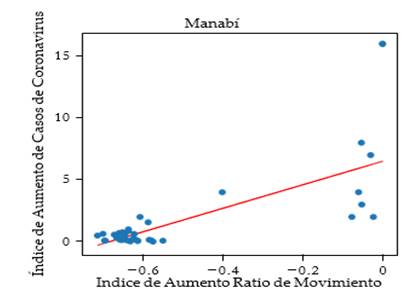
Figura 5. Resultado modelos predictivo contra datos de entrenamiento en Manabí.

Entonces, se consideró usar valores porcentuales como término dependiente o como valor a predecir, referido a ello como un índice o porcentaje de crecimiento, los cuales después de un breve cálculo permitirían obtener un rango de aumento de casos, obteniendo así el último modelo con los siguientes resultados:

Guayas

Muestra	ECM	R2
1	0.18	0.26
2	0.20	0.17
3	0.18	0.23
4	0.19	0.16
5	0.18	0.22

Tabla 14: Métricas de calidad de muestra en 5 iteraciones diferentes para el tercer modelo en la provincia de Guayas.

Manabí

Muestra	ECM	R2
1	1.30	0.00
2	1.23	0.01
3	1.29	0.00
4	0.09	0.05
5	1.30	0.00

Tabla 15: Métricas de calidad de muestra en 5 iteraciones diferentes para el tercer modelo en la provincia de Manabí.

Pichincha

Muestra	ECM	R2
1	0.26	0.31
2	0.23	0.35
3	0.04	0.06
4	0.01	0.06
5	0.25	0.32

Tabla 16: Métricas de calidad de muestra en 5 iteraciones diferentes para el tercer modelo en la provincia de Pichincha.

El error cuadrático medio es coherente al coeficiente de correlación de Pearson, dicho de otro modo, son valores concordantes que indican una precisión directamente relacionado a la correlación, que exista esta concordancia nos permite saber que el modelo no presenta errores para poder realizar la mejor predicción posibles, por ende, todo error al predecir el modelo solo está ligado a la dependencia de los nuevos casos de coranovirus con la ratio de movimiento.

El r2 presenta que el modelo es inestable, por lo cual la data no permitiría hacer un modelo de regresión lineal, debido a que es demasiado bajo su valor y más que una predicción mostraría un resultado aleatorio.

Estos modelos se probaron buscando siempre la mejor correlación para ajustarse a las variantes de cada región, siendo el último modelo el que mejores resultados tiene en comparación a los otros modelos, razón por la que es seleccionado para evaluar los resultados en la siguiente sección.

En el caso de las figuras [3, 4, 5], estas no muestran una correlación significativa. Hay valores muy dispersos y outliers que dificultan la precisión del modelo. Este modelo cumple con cierto rango de predicción, pero resulta muy aleatorio e impreciso. Aunque podemos apreciar con esto que este modelo es disfuncional.

DISCUSIÓN

Métricas de Calidad y Precisión

Error cuadrático medio

Al permitirse entender la cantidad de errores que presen- tan los modelos 1 y 2 al realizar una predicción, se dieron las bases para determinar un camino a seguir y así alcanzar un modelo óptimo. Los resultados que se arrojaban para los 2 primeros modelos con valores de ECM entre 2000 y 200000 en todos los subconjuntos de datos. Estos valores no co- rresponden a un modelo predictivo eficiente, lo que dio pie a buscar un modelo que subsanara este problema, siendo el modelo 3 donde se encontraría los resultados esperados para el modelo predictivo teniendo valores de ECM bajos, que fluctúan entre 0.18 y 1.30 para todos los subconjuntos de datos. Dicha mejora se concede al proceso en el que los datos fueron normalizados.

Coeficiente de correlación de Pearson

Este coeficiente de correlación fue un factor importante para la evaluación del tercer modelo debido a que, los valores de ECM son menores y están dentro del rango de aceptables para una buena predicción. Usando como ejemplo: Ecuador al intentar realizar una predicción con su menor coeficiente de correlación de Pearson (día 12) las predicciones mantienen resultados de 0,05; mientras que trabajar con datos con su mayor Coeficiente de correlación de Pearson (día 42) estas se elevan hasta el 0,25, datos que siguen siendo bajos para una predicción, pero que eleva significativamente la precisión del modelo. Para los modelos 1 y 2 no se tomó en cuenta esta métrica debido a que los resultados de ECM son mayores, lo que da indicio que la capacidad del modelo para predecir es ineficiente.

Coeficiente de determinación o r2

Este coeficiente evalúa la calidad del modelo para replicar los resultados. Al trabajar con el primer modelo los resultados de sus predicciones tendían a variar demasiado al repetir un mismo proceso predictivo. Teniendo en cuenta que sus resultados fueron de entre 0.01 hasta 0.16 para todos los subconjuntos de datos tras repetir un proceso de predicción con exactamente los mismos valores, la taza de confianza por ser tan inestable con sus resultados. Para el segundo modelo el problema de la estabilidad habría sido resuelto; mas sus resultados tan bajos teniendo un máximo valor de r²= 0.02, así como el resultado de las otras métricas dieron paso a cambiar el modelo, el tercer modelo tras un proceso de obtención de mejores conjuntos de datos se observaron resultados con una estabilidad adecuada y siendo lo más altos posible para la data rondando valores de r²= 0.60 como el pico máximo de predicción para los subconjuntos, datos que aun siendo altos comparados a los obtenidos previamente siguen siendo bajos mejorando la predicción del modelo.

Como se puede observar en la figura 6, en el caso del modelo aplicado en los países, específicamente en Argentina, presenta una creciente correlación entre casos positivos y ratio de Movimiento después del día 17, siendo su pico más alto el día 27. Este gráfico antes mencionado trata de expresar los días posteriores a la incubación, representando el tiempo de retraso en el que el virus es detectado. Factor que se consideró, ya que cada región funciona de forma independiente en base a la velocidad de detección que estos puedan presentar. Pero los resultados nos muestran que no existe una fuerte correlación con el movimiento debido a que, al inicio, el movimiento y el índice de contagio se muestran bajo un patrón parecido, pero estos se dispersan con el tiempo, reflejo de inexistencia en su dependencia, mostrándose como un patrón de casualidad y no de causalidad. Esto se puede ver representado en las figuras [3,4,5] de la sección anterior, en el que se muestran dichos valores o puntos de correlación de forma dispersa en las diferentes regiones del Ecuador, juntándose más puntos en la pendiente más baja. El mismo concepto de la figura 8, puede verse reflejado en las figuras [7 y 9], donde los datos están centrados en los casos provinciales, en las cuales se muestra una disminución en la correlación que pueda existir en base al avance de los días, ya que los datos son menos densos; aunque en algunos casos su pico más alto se encuentra entre el segundo y tercer día. [Figura 7].

Eficiencia de Modelos

Los primeros dos modelos presentaron un error cuadrático medio muy similar, siendo la media de 1895398, 27 para el primer modelo, y 2096580,40 para el segundo modelo. Datos muy elevados para esta métrica, reflejando imprecisión a grandes escalas; pero lo que marcó la diferencia en los resultados fue el tercer modelo que en cuanto a su rendimiento mostró más cercanía a los resultados espera- dos para un buen modelo, reflejados en los valores de las métricas de medición de calidad, donde el error cuadrático medio presenta un valor de 0, 19 teniendo en cuenta que ahora los valores se manejan en datos de 0 a 1. Pues pese a que muestran mejores valores, no son los adecuados para construir a un buen modelo. La correlación que se muestra se reflejan como valores de casualidad y no de causalidad al poseer valores que, con el tiempo y el crecimiento de datos, son más imprecisos.

Sudamérica

	Países	Correlación	Días
0	Argentina	0.53	27
9	Paraguay	0.53	24
2	Brasil	0.49	27
12	Uruguay	0.46	27
7	Guyana	0.45	25
5	Ecuador	0.43	29
1	Bolivia	0.42	26
10	Surinam	0.41	27
4	Colombia	0.37	29
11	Trinidad y Tobago	0.34	20
6	Guyana Francesa	0.31	19
3	Chile	0.25	26
8	Perú	0.24	16

Tabla 17: Datos de correlación más alta con respecto al movimiento que se tuvo por cada país.

Ecuador

	Provincias	Correlación	Días
11	Sucumbíos	0.82	3
17	Manabí	0.74	4
8	Pichincha	0.68	7
19	Morona Santiago	0.63	3
15	Guayas	0.56	14
23	Galápagos	0.53	14
1	Bolívar	0.41	0
6	Imbabura	0.37	0
4	Chimborazo	0.34	0
7	Loja	0.32	0
0	Azuay	0.27	0
2	Cañar	0.24	0
16	Los Ríos	0.23	0
13	Santo Domingo	0.22	0
10	El Oro	0.22	0
3	Carchi	0.15	0
22	Pastaza	0.14	0
14	Esmeraldas	0.07	0
5	Cotopaxi	0.06	0
18	Santa Elena	0.05	0
9	Tungurahua	0.05	0
20	Napo	-0.05	0
12	Zamora Chinchipe	-0.05	0
21	Orellana	-0.08	0

Tabla 18: Tabla de correlaciones por provincias del Ecuador.

Argentina

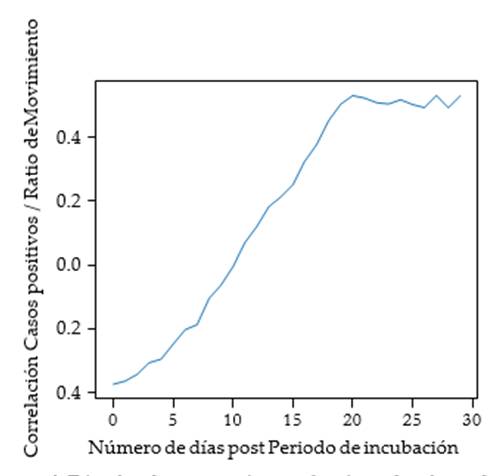
Figura 6. Días donde existe más correlación en los datos de Argentina

Guayas

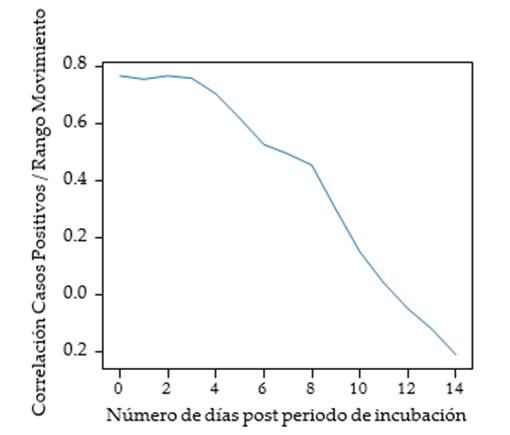
Figura 7. Número de días post período de incubación en la provincia de Guayas

CONCLUSIONES

Logros

A través de un análisis con los resultados de correlación entre distintos modelados de datos, se construyó un rango de periodo de incubación de 11 a 14 días (seleccionado como más preciso el día 12), siendo es- te una propiedad necesaria para mejorar el tiempo de detección de nuevos infectados.

De acuerdo al porcentaje de correlación por cada país en Latinoamérica y las provincias ecuatorianas, se comprendió qué tan relacionados está la movilidad y actividad humana con respecto a la cantidad de casos del coronavirus, con resultados desfavorables, demostrando que la movilidad no es un determinante para el contagio de este virus.

Se demostró que ciertas variantes tales como: periodo de incubación, índice o incremento porcentual de contagio y tiempo de retraso para detección de nuevos positivos; poseen un potencial existente para una mejor correlación y predicción de casos positivos del coronavirus.

Limitaciones

No se realizaron análisis más específicos debido a la falta de datos oportuno relacionados a regiones más centralizadas como ciudades.

Los movimientos obtenidos son relativos y no definitivos. Estos datos son un estimado extraído a través de la actividad vista en dispositivos, cuando se usa la red social “Facebook”.

Al no tener el movimiento relativo de los polígonos regionales a estudiar; existe la posibilidad de ruido o cambio de valores relativos al promediar dichos movimientos, adjunto a la falta de datos fiables de registros de casos positivos de contagios a tiempo real.

A pesar de existir más factores para desarrollar este estudio no se consideraron variables tales como “Números de pruebas” o “Probabilidad del roce”, que, en otros estudios referenciados si se consideran como su- puestos ¹⁴.

CONFLICTO DE INTERÉS

Los autores declaran que no tienen conflicto de interés en la publicación de este artículo.

FINANCIAMIENTO

Autofinanciado.

AGRADECIMIENTO

A la Universidad Técnica de Manabí, Portoviejo; por apoyar el desarrollo la investigación.

REFERENCIAS

1. Wang S, Guo L, Chen L, Liu W, Cao Y, Zhang J, Feng L. A Case Report of Neonatal 2019 Coronavirus Disease in China. Clin Infect Dis. 2020 Jul 28; 71(15):853-857. doi: 10.1093/cid/ciaa225. PMID: 32161941; PMCID: PMC7108144.

2. Díaz-Quijano FA, Rodríguez-Morales AJ, Waldman EA. Translating transmissibility measures into recommendations for coronavirus prevention. Rev. saúde pública [Internet]. 2020Apr.24; 540:43.

3. Pinedo Alonso, C. C. Corea del Sur, Japón y Singapur ¿ejemplos de éxito ante la covid-19? Pluraridad y Consenso, [Internet]. 2020. 10(44): 70-77.

4. Cadena-Estrada JC, Olvera-Arreola SS, López-Flores L, Pérez-Hernández E, Lira-Rodríguez G, Sánchez-Cisneros N, Quintero-Barrios MM. Nursing before COVID-19, a key point for the prevention, control and mitigation of the pandemic. Arch Cardiol Mex. 2020;90(Supl):94-99. English. doi: 10.24875/ACM.M20000058. PMID: 32523143.

5. Esakandari, H., Nabi-Afjadi, M., Fakkari-Afjadi, J. et al. A comprehensive review of COVID-19 characteristics. Biol Proced Online 22, 19 (2020). https://doi.org/10.1186/s12575-020-00128-2

6. Yushun Wan, Jian Shang, Rachel Graham, Ralph, S. Baric, Fang Li. Receptor recognition by the novel coronavirus from Wuhan: an analysis based on decade-long structural studies of SARS coronavirus. Journal of Virology Mar 2020, 94 (7) e00127-20; DOI: 10.1128/JVI.00127-20

7. World Health Organization. WHO. Clinical man- agement of severe acute respiratory infection (SARI) when COVID-19 disease is suspected. Ginebra: WHO; 2020

8. Burki T. COVID-19 in Latin America. Lancet Infect Dis. 2020 May;20(5):547-548. doi: 10.1016/S1473-3099(20)30303-0. Epub 2020 Apr 17. PMID: 32311323; PMCID: PMC7164892.

9. Arora P, Kumar H, Panigrahi BK. Prediction and analysis of COVID-19 positive cases using deep learning models: A descriptive case study of India. Chaos Solitons Fractals. 2020 Oct;139:110017. doi: 10.1016/j.chaos.2020.110017. Epub 2020 Jun 17. PMID: 32572310; PMCID: PMC7298499.

10. Lotfi M, Hamblin MR, Rezaei N. COVID-19: Transmission, prevention, and potential therapeutic opportunities. Clin Chim Acta. 2020 Sep;508:254-266. doi: 10.1016/j.cca.2020.05.044. Epub 2020 May 29. PMID: 32474009; PMCID: PMC7256510.

11. Ayyoubzadeh SM, Ayyoubzadeh SM, Zahedi H, Ahmadi M, R Niakan Kalhori S. Predicting COVID-19 Incidence Through Analysis of Google Trends Data in Iran: Data Mining and Deep Learning Pilot Study. JMIR Public Health Surveill. 2020 Apr 14;6(2):e18828. doi: 10.2196/18828. PMID: 32234709; PMCID: PMC7159058.

12. Humanitarian Data Exchange. HDX. [Online]; 2020 [cited 2020 October 08]. Available from: https://data.humdata.org/.

13. Christian Arias-Reyes, Liliana Poma Machicao, Fernanda Aliaga-Raduan, Danuzia A. Marques, Natalia Zubieta DeUrioste, Roberto Alfonso Accinelli, Edith M. Schneider-Gasser, Gustavo Zubieta-Calleja, Mathias Dutschmann, Jorge Soliz. Decreased incidence, virus transmission capacity, and severity of COVID-19 at altitude on the American continent. medRxiv 2020.07.22.20160168; doi: https://doi.org/10.1101/2020.07.22.20160168

14. Reeves JJ, Hollandsworth HM, Torriani FJ, Taplitz R, Abeles S, Tai-Seale M, Millen M, Clay BJ, Longhurst CA. Rapid response to COVID-19: health informatics support for outbreak management in an academic health system. J Am Med Inform Assoc. 2020 Jun 1;27(6):853-859. doi: 10.1093/jamia/ocaa037. PMID: 32208481; PMCID: PMC7184393.

15. Wissel BD, Van Camp PJ, Kouril M, Weis C, Glauser TA, White PS, Kohane IS, Dexheimer JW. An interactive online dashboard for tracking COVID-19 in U.S. counties, cities, and states in real time. J Am Med Inform Assoc. 2020 Jul 1;27(7):1121-1125. doi: 10.1093/jamia/ocaa071. PMID: 32333753; PMCID: PMC7188179.

16. Gibb, J., Back Propagation Family Album, Technical Report C/TR96-05, Macquarie University, August, 1996.

2020 por los autores. Este artículo es de acceso abierto y distribuido según los términos y condiciones de la licencia Creative Commons Atribución-NoComercial-CompartirIgual 4.0 Internacional (CC BY-NC-SA 4.0) (https://creativecommons.org/licenses/by-nc-sa/4.0/).