http://dx.doi.org/10.35381/r.k.v6i3.1339
Método Singapur y cuadernillo digital aplicado en la asignatura de matemáticas en Educación Básica
Singapore method and digital booklet applied in the subject of Mathematics in Basic Education
Jashmin Del Cisne Mullo-Pomaquiza
jashmin.mullo.28@est.ucacue.edu.ec
Universidad Católica de Cuenca, Azogues
Ecuador
https://orcid.org/0000-0001-5833-110X
Ana Zulema Castro-Salazar
Universidad Católica de Cuenca, Azogues
Ecuador
https://orcid.org/0000-0002-3837-314X
Recepción: 10 de abril 2021
Revisado: 05 de mayo 2021
Aprobación: 30 de junio 2021
Publicación: 15 de julio 2021
RESUMEN
El presente trabajo nace de la practica educativa, siguiendo la línea de investigación e innovación educativa. Se trabajó con una investigación de diseño no experimental, con un paradigma epistemológico cualitativo, en el cual se empleó una entrevista semiestructura mediante un grupo focal por la plataforma de Zoom a docentes de Educación Preparatoria, Elemental y Básica Media, en donde se consideró unidades de análisis, categorías y segmentos, donde se obtuvieron como resultados generales que los docentes tratan de innovar en sus clases sin considerar un modelo en específico y son limitados por el tiempo y la carga de trabajo por documentación. Por todo lo antes mencionado se realizó un cuadernillo digital de actividades para docentes con el método Singapur, enfocado en la enseñanza de la matemática, con el fin de mejorar la práctica educativa docente.
Descriptores: Matemáticas; análisis matemático; aprendizaje. (Palabras tomadas del Tesauro UNESCO).
ABSTRACT
This work is born from educational practice, following the line of educational research and innovation. We worked with a non-experimental design research, with a qualitative epistemological paradigm, in which a semi-structured interview was used through a focus group by the Zoom platform to teachers of Preparatory, Elementary and Middle Basic Education, where units of analysis, categories and segments, where it was obtained as general results that teachers try to innovate in their classes without considering a specific model and are limited by time and documentation workload. For all the aforementioned, a digital booklet of activities for teachers was made with the Singapore method, focused on the teaching of mathematics, in order to improve the educational practice of teachers.
Descriptors: Mathematics; mathematical analysis; learning. (Words taken from the UNESCO Thesaurus).
INTRODUCCIÓN
La investigación se enfoca en mejorar el proceso de formación e innovación educativa docente, a partir de nuevos y mejores métodos educativos, puesto que los resultados arrojados en la aplicación de la entrevista semiestructurada como instrumento de recolección de información mediante el grupo focal, muestra que los métodos usados están siendo escasos en la formación docente, y por ende está generando resultados promedios y no excelentes en el desarrollo social y cognitivo de los estudiantes de Educación Elemental, Preparatoria y Básica Media.
Además se presentaron las necesidades de cada docente quienes mencionan que no cuentan con material necesario y el tiempo para planear y aplicar diversas estrategias porque de parte del distrito solicitan demasiada documentación que limita el tiempo y esfuerzo de la planta docente al impartir e innovar una clase, viéndose en la penosa necesidad de no cambiar lo existente, recalcando la falta de interés de los estudiantes, la poca o nula innovación por parte de los docentes y un desarrollo de destrezas mecánico. Dando respuesta a la pregunta de investigación ¿Cómo mejorar la práctica docente en la enseñanza de matemática para los alumnos de la Educación Preparatoria, Elementa y Básica Media?
Se tiene por Objetivo General de la investigación: Realizar un cuadernillo digital de actividades para docentes con el método Singapur enfocado en la enseñanza de la matemática en la Educación Preparatoria, Elementa y Básica Media con el fin de mejorar la practica educativa docente. Con la hipótesis de que los estudiantes de la Educación Preparatoria, Elementa y Básica Media aprenden mejor matemática con el método Singapur.
Referencial teórico
El método Singapur ha sido tan exitoso en su país que ha logrado ser implementado en varios países asiáticos, norte americanos y latinoamericanos, considerando las necesidades de cada uno en el área de matemática (Juarez & Aguilar, 2018), en su investigación realizada en una escuela primaria pública del estado de Puebla en México, implementaron el método Singapur para la solución de problemas, con la finalidad de contribuir a la mejora de los aprendizajes de las matemáticas en educación primaria.
La metodología de investigación utilizada fue la cuantitativa y cualitativa pues se emplearon métodos cuantitativos (pre-test y pos-test) y cualitativas (observación participante), el diseño fue cuasi-experimental y la muestra fueron treinta y un niños de segundo año de una escuela. Los resultados mostraron que a partir de la aplicación del método Singapur los niños mejoraron los aprendizajes en matemáticas, pues siete de cada diez lograron resolver problemas de matemáticas que implicaban realizar una suma o una resta.
Por su parte, (Tapia-Reyes & Murillo-Antón, 2020), en su trabajo de investigación mencionan que, luego del análisis del alcance del método Singapur para la enseñanza de las matemáticas a partir de los enfoques, metodologías y teorías implementadas en países como: Perú, Colombia, Chile, y España, con concluyen que el Método Singapur ha incrementado positivamente el aprendizaje de las matemáticas, ya que permite a los estudiantes pasar de una fase manipuladora a una fase de dibujo, y gradualmente alcanzar un nivel abstracto, contemplando al método como un reto para los docentes que hoy no se desprenden del modelo educativo de enseñanza tradicional, cuya consecuencia es la presencia de alumnos desmotivados y con dificultades para el aprendizaje de las matemáticas.
Innovación educativa
La innovación educativa se define como la acción de crear, plantear y aplicar nuevas metodologías, herramientas educativas y métodos, en bienestar de la comunidad educativa centrado en la indagación de posibles soluciones a los problemas que se presentan en la educación. Además, se da a conocer como un cumulo de ideas, metodologías y estrategias nuevas o mejoradas, que tienen el fin de introducir y provocar cambios en las prácticas educativas vigentes y a futuro, por tanto, se asocia al cambio y se reconoce un componente oculto, ideológico, cognitivo, ético y afectivo (Sánchez & Escamilla, 2018).
Aportando con la idea anterior (Margalef-García & Arenas-Martija, 2006), mencionan que la innovación educativa es la implementación de un cambio significativo en el proceso de enseñanza-aprendizaje y en el clima institucional. En el proceso de enseñanza aprendizaje tiene una estrecha relación con la modificación y adaptación en los materiales utilizados, en los métodos, contenidos y contextos que implican la enseñanza, en cuanto al clima institucional se busca que el personal docente y los estudiantes estén en la capacidad de indagar, descubrir, reflexionar, criticar y cambiar de acuerdo a la situación que se presente en su diario vivir. Concordando con lo anterior es por ello que, se establece el buscar esa alternativa de apoyo al desarrollo cognitivo de los estudiantes y la mejora de la educación, siendo el método Singapur el más propicio.
Método Singapur
En 1980 el sistema educativo de Singapur introduce el enfoque de la enseñanza exitosa de las matemáticas enfatizado en lo Concreto-Pictórico y Abstracto (C-P-A). Para la década de 1990, vinculan dicho enfoque con la participación activa de los estudiantes (Meissner, 2015). Asimismo, en 1980 se plantea la resolución de problemas verbales utilizando el método modelo en educación básica, este método se basa en los modelos visuales, en la utilización de material concreto y en la práctica constante que ayuda a lograr una mejor comprensión profunda de los conceptos, el pensamiento lógico y la creatividad matemática (Alonso-Tello et al. 2013).
El objetivo del plan anual de matemáticas es reconocer a los estudiantes como sujetos autónomos de sus propios conocimientos, por lo tanto, están en la capacidad de aplicar los conceptos en la resolución de problemas en la vida real, desarrollar habilidades matemáticas, habilidades cognitivas y metacognitivas y desarrollar actitudes positivas hacia las matemáticas. El enfoque plantea cinco componentes integrales: conceptos, habilidades, procesos, actitudes y metacognición (Har, 2009).
Actualmente, se considera que los niños no deben aprender por repetición y son considerados como agentes activos, estudiantes responsables que construyen lo que le enseñan de manera personal y significativa. En este sentido es el profesor quien debe proveer de oportunidades diversas de aprendizaje siempre retomando los conocimientos previos avanzando al mismo tiempo que amplía el conocimiento, se habla directamente del “currículum en espiral” (Alonso-Tello et al. 2013). Por otro lado, el enfoque Concreto-Pictórico-Abstracto es una pedagogía adoptada de los textos de matemáticas primarias desde 1980. A continuación, se detallan las fases del enfoque:
- Concreto, se enfoca en trabajar con actividades relacionadas con la vida real y el contexto del estudiante con la finalidad de acercar a los conceptos matemáticos. En este eje se trabaja la participación activa y el aprendizaje autónomo, pues los estudiantes son quienes construyen su propio aprendizaje por medio de la manipulación.
- Icónico o pictórico, es necesario dibujar o representar en un modelo ilustrado o pictórico las cantidades matemáticas conocidas y las desconocidas. Después se las debe comparar en un problema para visualizar y poder resolver el problema. En lo pictórico el estudiante trabaja el pensamiento lógico, pues debe ilustrar lo contenido en el texto presentado para la resolución de problemas y cuestionamientos.
- Abstracto, los estudiantes en lo abstracto estructuran algoritmos al usar signos y símbolos matemáticos que integran lo encontrado en la fase concreta e icónica. En esta fase se trabaja la comprensión de los conceptos y el pensamiento lógico pues debe relacionar lo trabajado en el eje concreto y pictórico para construir su propio concepto (Alonso-Tello et al. 2013).
Eventualmente, en la etapa abstracta los estudiantes pueden resolver problemas sin dibujar los modelos, puesto que son una ayuda visual y no es necesario que los estudiantes describan o expliquen el modelo que construyeron. El modelado matemático es un proceso de representación de problemas de la vida real en términos matemáticos con la finalidad de solucionar esos problemas. El docente prepara la clase considerando un problema real y lo adapta al año de básica, formulando el problema matemático que puede ser resuelto utilizando cualquier técnica conocida para encontrar una solución matemática. Luego, esta solución se interpreta y se traduce en términos reales.
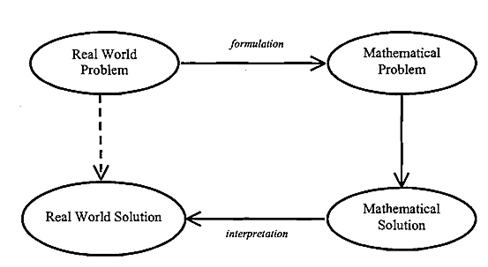
Figura 1. Proceso del modelo Matemático
Fuente: West (1998).
Cuadernillo de actividades
El cuadernillo de actividades es un documento en el que se recopilan actividades con fines educativos, que contienen una gama de ejercicios que son creados, organizados y recopilados para apoyar a la estimulación de funciones mentales. El cuadernillo tiene una parte informativa (contenido del tema) y una directiva (actividades a realizarse). La ficha informativa se presenta mediante organizadores gráficos y otras técnicas para sintetizar el contenido, tornándose más atractivo y de fácil entendimiento. En cuando a la ficha directiva se especifican las actividades contemplando los momentos de un período de clase, actividades que irán direccionadas con el método Singapur y realidad educativa (Unidad de Educación Especial de la Subdirección General de Servicios Educativos, del Instituto Estatal de Educación Pública de Oaxaca, 2020)
METODOLOGÍA
La presente investigación fue de diseño no experimental, puesto que se realizó un análisis de los datos obtenidos, más no una intervención por parte de la investigadora, por ello, la investigación gira entorno a un paradigma epistemológico cualitativo, en el cual se trabajó con una entrevista semiestructura mediante un grupo focal por la plataforma de Zoom, en donde se consideró las siguientes unidades de análisis: Desarrollo de la asignatura de matemática, recursos didácticos, Método Singapur, grupo focal, docencia y resultados de aprendizaje , cada uno con sus categorías y segmentos, mismo que fueron analizados minuciosamente. Es por esto que, se trabajó con una cohorte transversal al recolectar los datos en una sola cohorte de tiempo.
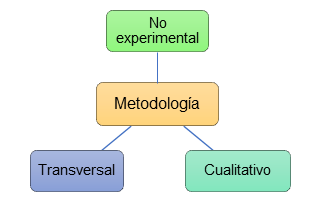
Figura 2. Metodología
Elaboración: Los autores.
La investigación se desarrolló en el área de Matemática en la Educación Preparatoria, Elementa y Básica Media de un Escuela Particular de la Ciudad de Gualaceo - Azuay – Ecuador. En la actualidad, la institución oferta a los moradores de la zona, una educación en los niveles: preparatoria, educación básica con los subniveles media y elemental. Actualmente, existe un paralelo para cada grado de los subniveles antes mencionados, con una planta docente y administrativa de 11 profesionales en Educación y 112 estudiantes. El marco muestral se definió de acuerdo a un muestreo aleatorio simple, con un total de 4 docentes que laboran en la Educación, Preparatoria (1), Elemental (2) y Básica Media (1).
Por consiguiente, el instrumento utilizado fue la entrevista semiestructurada que “se enmarca dentro del quehacer cualitativo como una herramienta eficaz para desentrañar significaciones, las cuales fueron elaboradas por los sujetos mediante sus discursos, relatos y experiencias. De esta manera se aborda al sujeto en su individualidad e intimidad” (Troncoso-Pantoja & Amaya-Placencia, 2017, p. 239), contando con un protocolo de entrevista (11 preguntas abiertas), como instrumento validado por expertos en el área. De la mano se desarrolló un grupo focal que “es una técnica de recolección de información mediante una conversación o discusión grupal semiestructurada, que está centrada en un tema propuesto por el investigador” (López-Francés, 2010, p. 59).
El protocolo de entrevista tuvo la finalidad de recabar información verídica a docentes de Preparatoria, Educación General Básica elemental y media, por medio de entrevistas semiestructuradas, con el fin de conocer acerca de la práctica educativa docente actualmente aplicada en el área de Matemática. Constó de 11 preguntas abiertas.
RESULTADOS
El análisis de los datos obtenidos arroja que: en el desarrollo de la asignatura de Matemática, mencionan acerca de los momentos de la clase que usan en su práctica diaria siendo: la anticipación, construcción y consolidación, en donde se hace hincapié en la consolidación con la manipulación de material concreto, luego pasan a la parte simbólica y abstracta. También trabajan con la resolución de problemas a partir del método de Polya, el método de Singapur, con el aumento de complejidad y método Montessori con la noción de contar, trazos y escritura.
En cuanto a los recursos didácticos, utilizan material didáctico concreto como: los cuentos porque parten del contexto hacia la identificación del contenido, de igual manera el uso de títeres, la máquina de suma, títeres que representar símbolos, materiales de fácil acceso en los hogares (granos secos o alimentos), regletas con palos de helado, juguetes que tienen en el hogar, tarjetas de valor posicional, cajita mackinder, Así mismo, el uso de herramientas digitales: videos, juegos digitales-online y las redes sociales.
En relación con el trabajo memorístico no se trabaja con los estudiantes de preparatoria, puesto que se debe razonar y relacionar el contenido mediante los pictogramas, por otro lado, en segundo de básica se utiliza la parte memorística y más aún en matemáticas al aprender los números, su orden y las secuencias, ero se podría decir que para llegar a ser memorísticos se debe partir de la relación con objetos, adicionalmente en tercero de básica se busca que sea un aprendizaje significativo a partir de la parte memorística, así mismo en quinto año es fundamental el uso de la memoria para la comprensión de las multiplicaciones y luego de las divisiones, es una relación de la memorístico con la comprensión a largo plazo, es importante el trabajar con el aprendizaje memorístico.
Todavía cabe señalar acerca del currículo en espiral, que no se sabe a ciencia cierta de que se trata, pero, a partir del nombre se menciona que es proceso que avanza dependiendo del año de básica. Por otro lado, la docente de quinto año menciona que se relaciona con el método Singapur en donde se menciona que los conocimientos se van tratando en espiral, en donde se trata de retomar los conocimientos y se refuerzan de acuerdo a la edad de los niños y el tema a tratar.
Además, se trató sobre la comprensión conceptual, que se relaciona con los cuentos y canciones para asimilar conocimientos, de igual manera como relacionamos los conceptos con los problemas, en donde los estudiantes inconscientemente crean sus conceptos, puesto que aprender haciendo. En el caso de tercero los estudiantes analizan los procesos y logran crear conceptos a partir de su práctica y problemas conceptuales. La resolución de problemas es el más usado en quinto año, para aplicar los conceptos en otros problemas, también los juegos ayudan para apropiarse de los conceptos.
Con respecto a la resolución de problemas en primer año se realiza en base a vivencias de los estudiantes y los nombres, asimilando los contenidos con ayuda de pictogramas. En quinto de básica se manejan a partir de 4 pasos: comprensión del problema, pensar una estrategia (¿Qué dedo hacer?), operación y respuesta, de igual manera el problema está contextualizado a la realidad del estudiante para que sea más fácil la comprensión, con el manejo de gráficos y pictogramas, además, con el uso de material concreto y la información que trae el libro acerca del método Singapur.
En tercero se resuelve con ayuda del docente, analizando el problema y contextualizándolos porque es más atractivo, los niños comprender si los vinculan con el material concreto, luego analizar, resuelven y presentan los resultados. En quinto se usa el método de Polya: comprende el problema, se plantea una forma de resolver el problema, se pone en práctica el plan y se analiza la respuesta que se obtiene, se toma en cuenta las 3 fases del método Singapur concreto pictórico y abstracto. El siguiente punto trata del uso del método Singapur, tiene mucho que ver con el método de Polya que presenta los textos con la diferencia de, que es más gráfico a través de pictogramas con el razonamiento de los estudiantes de forma gráfica sin necesidad de hacer la operación, considerando el aprendizaje significativo.
De igual modo se analiza lo mencionado de acuerdo al aprendizaje autónomo que se trata de que el estudiante aprende por si solo con ayuda del docente, en primer año se utiliza los cuentos en donde se plasma el contenido a trabajar, asimilando la secuencia, en segundo ese aprendizaje logra que los estudiantes sean más independientes, sean actores de su aprendizaje, permite que los estudiantes aprendan a su realidad y ritmo, la función del docente con las actividades planteadas para que el estudiante logre construir su conocimiento y los pueda aplicar cotidianamente. En tercero los estudiantes creen por si solos su proceso de aprendizaje y avanzan, se enfoca también con el nivel de responsabilidad de cada niño.
En quinto el estudiante indaga e investiga por sí solo, aprendiendo nuevos conocimientos, a partir de la práctica y deducen que será el siguiente tema y lo aplican en problemas combinados de acuerdo a lo aprendido anteriormente. Hay que mencionar también que el grupo focal enriquece la experiencia docente por el intercambio de ideas, mejorando el proceso educativo y la actualización docente. Se debe agregar que la innovación educativa no se ha logrado en la vida profesional del docente por la falta de tiempo y la excesiva documentación solicitada. Siguiendo la línea es importante mantenerse actualizado por el sinnúmero de cambios en la sociedad y más aún en el ámbito educativo. Es por esto que el nivel de aprendizaje de los estudiantes se ha visto afectado al no obtener resultados excelentes y mantenerse en un promedio.
En consecuencia, las docentes participantes en el grupo focal, realizan actividades relacionadas con el Método Singapur más no conocían el método en su totalidad (fases concreta, pictórica y abstracta), a excepción de la docente de quinto que ha procurado trabajar con ello. Se puede destacar la labor docente que han consiguiendo que los estudiantes se mantengan en un nivel promedio de desarrollo de destrezas en el área de matemática, con las escasas bases del método Singapur.
Tabla 1.
Grupo focal. Docente de Educación Elemental, Preparatoria y Básica Media.
|
Unidad de análisis |
Categoría |
Segmento |
|
Desarrollo de la asignatura de matemática. |
Momentos de la clase de matemáticas. |
- Anticipación, construcción y consolidación.
|
|
|
Metodologías usadas durante la clase de matemática |
- Resolución de problemas con el método de Polya (4 Pasos: comprensión del problema, pensar una estrategia, operación y respuesta). - Singapur (concreto, pictórico y abstracto). - Método Montessori (Noción de contar, trazos, conteo de cantidades y escritura).
|
|
|
Complejidad |
- De acuerdo al año de básica |
|
|
|
- De acuerdo al tema |
|
Recursos didácticos |
Material didáctico concreto |
- En la construcción - Caja Mackinder - Cuentos - Títeres - Máquina de la suma - Tarjetas del valor posicional - Texto - Materiales de fácil acceso en los hogares (alimentos) - Se trata de construir la mayor cantidad de material a pesar del tiempo limitado.
|
|
|
Herramientas digitales |
- Videos educativos - Juegos Online - Redes sociales
|
|
|
Trabajo memorístico |
- Se utiliza muy poco la memoria cuando de sebe razonar - Se vincula con los pictogramas - Se presenta con la relación entre los objetos y el contenido - Se da en el aprender los números y su secuencia - Es indispensable al aprender la multiplicación - No se puede excluir del currículo
|
|
Método Singapur |
Aprendizaje significativo |
- Asimilación de contenidos - Gráfico con el uso de pictogramas - Representar algo abstracto en gráfico |
|
|
Currículo en espiral |
- No se conoce del tema - Es un proceso - Avanza de año en año - Mayor complejidad - Método de Singapur - Se retoma el conocimiento para reforzarlo
|
|
|
Comprensión conceptual |
- A partir de un cuento se da a conocer el contenido - Relacionamos el concepto con la simbología - Creación de conceptos de acuerdo a lo que van haciendo - Aprender haciendo - Situaciones problema - Resolución de problemas - Aplicación de conceptos - Juegos - Apropiación de conceptos |
|
|
Resolución de problemas |
- En base a vivencias - Pictogramas - Preguntas - Método Singapur: Concreto, abstracto y simbología. - Con material concreto - Método de Polya 4 Pasos: comprensión del problema, pensar una estrategia, operación y respuesta. |
|
|
Aprendizaje autónomo |
- El estudiante aprende por sí solo - Construyen sus hábitos de aprendizaje de acuerdo a su ritmo - Independencia por parte de los estudiantes - Los aprendizajes son aplicables - Buscan avanzar más de lo habitual - El niño a partir de su propia iniciativa aprende más acerca de un tema. - Relacionar los temas interiorizados con los nuevos |
|
|
Representación gráfica |
- Mediante pictogramas, dibujos y gráficos - Semirrecta numérica - Ayuda a interiorizar el contenido - Se relaciona con la vida diaria - Es necesario ejemplificar con problemas del contexto - Es útil porque llama mucho la atención del estudiante.
|
|
Grupo focal |
Experiencia docente |
- Intercambio de ideas - Mejora el proceso educativo - Ayuda en la actualización docente - Actualización en educación
|
|
Docencia |
Innovación |
- Falta de tiempo por la presentación de documentación excesiva. - Poca accesibilidad a material - Importante para adaptarse al contexto |
|
Resultados de aprendizaje |
Estudiantes |
- Nivel promedio mas no excelente |
|
|
|
|
Fuente: Entrevistas.
Dando fiabilidad a la aplicación del método Singapur en matemáticas podemos afirmar que, el método Singapur permitió a los niños resolver problemas matemáticos siguiendo una serie de pasos los cuales propiciaban llegar a la solución del problema. Si esta estrategia se aplicara desde el inicio del ciclo escolar se lograrían mejores resultados en el área de matemáticas (Juarez & Aguilar, 2018). De la misma forma, los resultados permitieron mostrar un impacto positivo en el logro de los aprendizajes y desarrollo de habilidades matemáticas en estudiantes de 4° básico que utilizan el Método Singapur respecto de estudiantes del mismo nivel que utilizan otras metodologías de enseñanza de las matemáticas. Además, se verificó una reducción estadísticamente significativa en la brecha de género de los estudiantes que vivieron la aplicación del MS (Espinoza et al., 2018).
A partir de lo mencionado se pretende realizar un cuadernillo digital de actividades para docentes con el método Singapur, enfocado en la enseñanza de la matemática en la Educación Preparatoria, Elementa y Básica Media con el fin de mejorar la practica educativa docente.
PROPUESTA
CUDIMESI (Cuadernillo digital con el Método Singapur).
¿Cómo mejorar la práctica docente en la enseñanza de matemática para los alumnos de la Educación Preparatoria, Elementa y Básica Media?, dando respuesta a la pregunta de investigación se plantea la creación de un cuadernillo digital con actividades enfocadas en las 3 fases del método Singapur: concreto, pictórico y abstracto, con el fin de mejorar la practica educativa docente y apoyar a la innovación en el marco educativo.
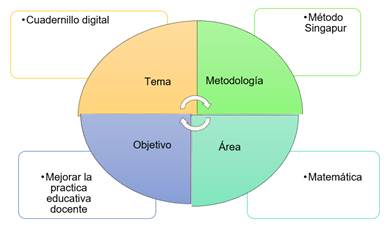
Figura 3. Propuesta CUDIMESI.
Elaboración: Los autores.
Los pasos para llevar a cabo la propuesta se delimitan en:

Figura 4. Pasos para realizar la propuesta.
Elaboración: Los autores.
La propuesta contempla una evaluación formativa por tema de clase, además es fiable y no tiene costo. Algunos de los aspectos a considerar para el éxito de la propuesta es: Evitar en lo posible la repetición, dirigir las actividades e torno a: Indagar, describir, reflexionar, criticar, cambiar o modificar, crear, construir y Autoeducar.
Se adjunta el link del cuadernillo digital: https://www.flipsnack.com/JashminMullo/newflipbook.html
CONCLUSIONES
El método Singapur centra su éxito en tres fases enlazadas la uno de la otra y en secuencia, partiendo de lo concreto, seguido de lo pictórico y finalizando con lo abstracto, abreviando C - P – A, fomentando la creación de material concreto y la práctica continua para mejorar la comprensión de los conceptos, enriquecimiento del pensamiento lógico y profundización de una matemática creativa e innovadora. Durante el desarrollo del método el docente es un guía que diseña e implementa actividades centradas en situaciones problemáticas contextualizadas para que el estudiante sea quien descubra de forma autónoma el proceso y recursos que debe usar para su resolución y presentación.
Por consiguiente, se trabajó con un diseño no experimental, puesto que se realizó un análisis de los datos obtenidos, por ello, la investigación giró en torno a un paradigma epistemológico cualitativo, en el cual se trabajó con una entrevista semiestructura mediante un grupo focal por la plataforma de zoom, con una cohorte transversal al recolectar los datos en 1 sola cohorte de tiempo. Arrojando como resultados que los profesores han buscado la forma de innovar las clases, pero el tiempo de planeación es uno de los factores que limita esta labor docente, además los estudiantes requieren nuevas y mejores metodologías que estén a la vanguardia con su desarrollo social y cognitivo.
En conclusión, la propuesta es fiable por que abarca aspectos tales como un cuadernillo digital de fácil acceso al público, mismo que se estructura mediante fichas informativas y directivas que se estructuran con el método Singapur a partir de actividades que desarrollan la autonomía, pensamiento lógico, comprensión- construcción de conceptos y resolución de problemas, contemplando que ayudará con la formación educativa docente con un enfoque innovador y actualizado.
FINANCIAMIENTO
No monetario.
AGRADECIMIENTO
A la Jefatura de Posgrados de la Universidad Católica de Cuenca por permitir el desarrollo y fomento de la investigación.
REFERENCIAS CONSULTADAS
Alonso-Tello, C., López Barriga, P., & Cruz Vicente, O. (2013). Creer tocando [Believe by touching]. Tendencias Pedagógicas, 21(21), 249–262. https://n9.cl/duo82
Espinoza, L., Matus, C., Barbe, J., Fuentes, J., & Márquez, F. (2018). Qué y cuánto aprenden de matemáticas los estudiantes de básica con el método Singapur: evaluación de impacto y de factores incidentes en el aprendizaje, enfatizando en la brecha de género [What and how much do elementary school students learn about mathematics with the Singapore method: evaluation of impact and incident factors in learning, emphasizing the gender gap]. Calidad en la Educación, (45), 90-131. https://doi.org/10.31619/caledu.n45.16
Har, Y. B. (2009). The Singapore Mathematics Curriculum and Mathematical Communication. https://n9.cl/32ayn
Juarez, M. del R., & Aguilar, M. (2018). El método Singapur, propuesta para mejorar el aprendizaje de las Matemáticas en Primaria [The Singapore method, proposed to improve the learning of Mathematics in Primary]. Números, 98(12), 75–86. https://n9.cl/thk1
López-Francés, I. (2010). El grupo de discusión como estrategia metodológica de investigación: aplicacióna un caso [The discussion group as a methodological research strategy: application to a case]. Edetania. Estudios Y Propuestas Socioeducativos., (38), 147-156.
Margalef-García, L, & Arenas-Martija, A. (2006). ¿Qué entendemos por innovación educativa? A próposito del desarrollo curricular [What do we understand by educational innovation? For the purpose of curriculum development]. Perspectiva Educacional, Formación de Profesores, (47),13-31.
Meissner, H. (2015). Creativity in Mathematics Education [Creatividad en la educación matemática]. The Proceedings of the 12th International Congress on Mathematical Education, 591–592. https://doi.org/10.1007/978-3-319-12688-3_64
Sánchez, M., & Escamilla, J. (2018). Perspectivas de la innovación educativa en universidades de México: experiencias y reflexiones de la RIE 360 [Perspectives of educational innovation in Mexican universities: Experiences and reflections of the RIE 360]. https://n9.cl/r4lgn
Tapia-Reyes, R. A., & Murillo-Antón, J. (2020). El método Singapur: sus alcances para el aprendizaje de las matemáticas [The Singapore method: its scope for learning mathematics]. Revista Muro de La Investigación, 5(2), 13–24. https://doi.org/10.17162/rmi.v5i2.1322
Troncoso-Pantoja, C., & Amaya-Placencia, A. (2017). Interview: A practical guide for qualitative data collection in health research [Entrevistas guía práctica para la recolección de datos cualitativos en investigación de salud]. Revista Facultad de Medicina, 65(2), 329–332. https://doi.org/10.15446/revfacmed.v65n2.60235
Unidad de Educación Especial de la Subdirección General de Servicios Educativos, del Instituto Estatal de Educación Pública de Oaxaca. (2020). Cuadernillo de actividades para estimular las funciones mentales superiores. Trabajo pedagógico a distancia 2020 [Activity booklet to stimulate higher mental functions. Distance pedagogical work 2020]. Recuperado de https://n9.cl/711z
West, E. (1998). Teaching and learning mathematical modelling, by S. K. Houston, W. Blum, I. Huntly and N. T. Neill. Pp. 401. £36.50. 1997. ISBN 1-898563-29-2 (Albion). The Mathematical Gazette, 82(493), 158-158. doi: 10.2307/3620196
©2021 por los autores. Este artículo es de acceso abierto y distribuido según los términos y condiciones de la licencia Creative Commons Atribución-NoComercial-CompartirIgual 4.0 Internacional (CC BY-NC-SA 4.0) (https://creativecommons.org/licenses/by-nc-sa/4.0/).