https://doi.org/10.35381/i.p.v6i11.4158
Suavizado
de curvas para ajustar datos con estructura no lineal desde la perspectiva
p-splines
Curve smoothing for fitting data with nonlinear structure
from a p-splines perspective
Maryorys Verónica Polanco
maryorysp@gmail.com
Universidad Nacional Experimental Francisco de Miranda, Santa
Ana de Coro, Falcón
Venezuela
https://orcid.org/0000-0002-2641-1671
Recepción:
10 de marzo 2024
Revisado:
15 de mayo 2024
Aprobación:
15 de junio 2024
Publicado:
01 de julio 2024
RESUMEN
El
objetivo de este trabajo fue realizar una aproximación teórica de carácter
documental, descriptivo y aplicado al enfoque de la teoría de aproximación
P-splines. La metodología utilizada incluye, primeramente, una revisión
documental que permitió identificar las principales características del método
y los enfoques existentes; segundo, la etapa experimental que consistió en
ajustar seis series de datos provenientes del estudio sobre la dinámica
poblacional de Ralstonia Solanacearum en plantas de tomate mediante el software
R-Project y, por último, los resultados obtenidos. Se evidenció que el
parámetro 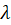 es el responsable de
controlar el suavizado y en la búsqueda de un valor para este parámetro que
optimice el ajuste, se puede confiar en el estimado por la función GAM, ya que
proporcionó ajustes casi idénticos a los modelos con un valor de
es el responsable de
controlar el suavizado y en la búsqueda de un valor para este parámetro que
optimice el ajuste, se puede confiar en el estimado por la función GAM, ya que
proporcionó ajustes casi idénticos a los modelos con un valor de 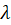 asignado que de
acuerdo a los criterios e índices considerados, fueron seleccionados como
modelo final.
asignado que de
acuerdo a los criterios e índices considerados, fueron seleccionados como
modelo final.
Descriptores: Análisis
estadístico; suavizado; datos; series (Tesauro UNESCO).
ABSTRACT
The
objective of this work was to conduct a theoretical, descriptive, and applied
documentary approach to the P-splines approximation theory. The methodology
employed included, firstly, a literature review to identify the main
characteristics of the method and existing approaches; secondly, an
experimental stage consisting of fitting six data series from a study on the
population dynamics of Ralstonia Solanacearum in tomato plants using the
R-Project software; and finally, the obtained results. It was evident that the
parameter λ is responsible for controlling the smoothing, and in
the search for a value for this parameter that optimizes the fit, one can rely
on the estimate provided by the GAM function, as it provided almost identical
fits to the models with an assigned value of λ, which, according to the considered
criteria and indices, were selected as the final model.
Descriptors: Statistical analysis; smoothing; data; series. (UNESCO Thesaurus).
INTRODUCCIÓN
El suavizado de curvas es una técnica estadística
fundamental para modelar relaciones no lineales entre variables. En este
contexto, los P-splines han emergido como una herramienta poderosa y flexible.
Este análisis argumentativo explorará en profundidad las ventajas y
aplicaciones de los P-splines en el suavizado de datos con estructura no
lineal, así como sus limitaciones y consideraciones.
Un spline es la solución a un problema de
optimización. Para Ramírez y Polack (2020) puede ser considerada “como
una técnica de estimación de funciones no paramétricas” (p. 194). En un sentido
real, los splines representan una evolución de la inferencia estadística
clásica y cierra la brecha entre los métodos paramétricos y no paramétricos.
Los P-splines son una extensión de los splines tradicionales, combinando la
flexibilidad de las bases de splines con la regularización de las diferencias
de orden superior de los coeficientes de la spline. Esta combinación permite
obtener ajustes suaves y flexibles a los datos, al tiempo que evita el
sobreajuste (Barrientos et al., 2007).
Una técnica no paramétrica basada en
splines, que permite ajustar datos sin que sea necesario conocer la relación
que guardan las variables, se conoce como P-splines y fue introducida por
primera vez con este nombre por Eilers y Marx (1996) para cubrir la combinación
de B-splines y una penalidad de diferencia discreta cuyas propiedades son muy
atractivas. Vale destacar, que existe una base para el conjunto de splines
naturales llamada base B-spline la cual está formada por trozos de polinomios
conectados entre sí. En general, un B-Spline de grado 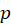 consiste
en p+1 trozos de polinomios de grado
consiste
en p+1 trozos de polinomios de grado 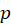 que
se unen en
que
se unen en 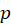 nodos
internos (Salas et al., 2010).
nodos
internos (Salas et al., 2010).
Por su parte, Durbán (2009) expresa que “los
factores que han hecho que esta técnica haya alcanzado tanta popularidad en los
últimos años han sido la creciente complejidad de los datos con los que se
trabaja” (p. 197), y los avances informáticos que han facilitado el ajuste de
este tipo de modelos, reduciendo significativamente el costo computacional. Es
por ello, que, desde su aparición, un poco más de veinte años, se han vuelto
populares en aplicaciones y en trabajos teóricos, ya que la combinación de una
base B-spline y una penalidad se prestan para una variedad de generalizaciones,
porque se basa en la regresión.
Por lo anterior, es evidente que los
P-splines representan una buena solución para la estimación de la función
regresora por dos razones: la primera, es su flexibilidad para responder a la
variación local sin permitir comportamientos patológicos, y segundo, el actual
grado de suavidad es controlable. Aun cuando el grado de suavidad correcto es
desconocido, estas características junto con el método de validación cruzada
permiten un ajuste no paramétrico, de allí, que se haya convertido rápidamente
en una técnica popular de suavizado, debido a su simplicidad y flexibilidad en
el manejo de una amplia gama de situaciones de modelado no paramétrico y
semiparamétrico (Toriz y Sánchez, 2017).
La idea principal de la estimación
P-spline se basa en emplear una base dimensional grande pero finita; esta
versión penalizada proporciona un ajuste suave a diferencia del ajuste
paramétrico simple, que conduciría a estimaciones variables y ondulantes.
En cuanto a las aplicaciones, el hecho de que
los P-splines se puedan escribir como un modelo mixto, proporciona ventajas en
dos ámbitos distintos: por un lado, hace que se pueda flexibilizar la hipótesis
de linealidad en infinidad de modelos, y por otro, es posible incluir
estructuras complejas en los modelos usuales de suavizado. Otra área en el que
los P-splines están tomando un papel relevante es en el análisis de datos
longitudinales, tan frecuentes en aplicaciones médicas y biológicas, aquí, los
P-splines permiten ajustar modelos más flexibles en los que las diferencias
específicas individuales son una función suave del tiempo (Álvarez et al., 2015).
De acuerdo con lo descrito en las ideas anteriores, este trabajo de
investigación tuvo como objetivo principal aplicar el método de aproximación
P-splines para suavizado de curvas en presencia de datos con estructura no
lineal.
MÉTODO
Para
aplicar e ilustrar la técnica de suavizado enfocado en Psplines, se utilizaron
datos reales proporcionados por Lugo (2018), correspondientes a su tesis
doctoral titulada “Efecto de Bacterias Antagonistas y Extractos
Vegetales sobre la Dinámica Poblacional de Ralstonia Solanacearum (Smith)
Yabuuchi et al. y la Expresión de Síntomas en Tomate (Solanum
Lycopersicum l.)”
Para
la obtención de R. solanacearum se planificó un experimento en un diseño
completamente aleatorizado, con cinco tratamientos y tres réplicas. La unidad
experimental consistió de una maceta de 1500 g de capacidad (una planta por
maceta). Los tratamientos se describen en la tabla 1.
Tabla 1.
Tratamientos del
experimento para la obtención de R. solanacearum.
|
TRATAMIENTO
|
CARACTERÍSTICA
|
|
1
|
Plantas
control. Sin inoculación de la bacteria.
|
|
2
|
Plantas
control. Plantas inoculadas solo con R. solanacearum.
|
|
3
|
Plantas
inoculadas con R. solanacearum y tratadas con extracto acuoso de R. communis
(Tártago).
|
|
4
|
Plantas
inoculadas con R. solanacearum y tratadas con la bacteria antagonista P
fluorescens.
|
|
5
|
Plantas
inoculadas con R. solanacearum y tratadas con el producto comercial Timorex.
|
Fuente: Lugo (2018).
La
medición del tamaño de la población de R. solanacearum en el suelo,
medido en UFC/g de suelo se hizo cada semana, es decir, 20 mediciones de la
variable, las cuales se muestran en la tabla 2.
Tabla
2.
Población
promedio de Ralstonia solanacearum en el suelo, medido en UFC*106
por g de suelo.
|
DIA
|
T1
|
T2
|
T3
|
T4
|
T5
|
TOTAL
|
|
0
|
0,172
|
0,756
|
1,233
|
0,039
|
7,556
|
1,951
|
|
7
|
0,094
|
0,217
|
2,672
|
0,328
|
14,106
|
3,483
|
|
14
|
0,372
|
2,072
|
7,322
|
0,772
|
9,728
|
4,053
|
|
21
|
0,589
|
1,644
|
8,322
|
0,683
|
10,528
|
4,353
|
|
28
|
0,839
|
2,661
|
8,567
|
1,622
|
16,200
|
5,978
|
|
35
|
1,389
|
2,417
|
11,789
|
1,867
|
17,233
|
6,939
|
|
42
|
1,039
|
2,650
|
12,944
|
1,844
|
12,967
|
6,289
|
|
49
|
1,656
|
1,639
|
13,472
|
2,511
|
15,794
|
7,014
|
|
56
|
1,100
|
2,617
|
10,950
|
2,106
|
15,244
|
6,403
|
|
63
|
0,672
|
1,211
|
11,033
|
2,639
|
12,094
|
5,530
|
|
70
|
0,906
|
0,656
|
10,172
|
2,989
|
10,311
|
5,007
|
|
77
|
1,194
|
1,239
|
12,494
|
2,061
|
12,550
|
5,908
|
|
84
|
0,750
|
0,456
|
12,217
|
2,478
|
9,439
|
5,068
|
|
91
|
0,833
|
0,661
|
13,378
|
1,933
|
9,139
|
5,189
|
|
98
|
1,428
|
1,022
|
10,906
|
2,533
|
8,039
|
4,786
|
|
105
|
1,733
|
1,011
|
9,394
|
1,606
|
7,278
|
4,204
|
|
112
|
1,267
|
0,911
|
10,117
|
1,706
|
8,039
|
4,408
|
|
119
|
1,361
|
0,994
|
7,283
|
1,461
|
5,278
|
3,275
|
|
126
|
1,761
|
0,950
|
11,222
|
1,944
|
5,706
|
4,317
|
|
133
|
1,389
|
0,617
|
6,356
|
1,206
|
5,128
|
2,939
|
Fuente: Lugo (2018).
Para
obtener los modelos matemáticos que describen la dinámica poblacional en el
suelo de R. solanacearum bajo las condiciones descritas, el autor
utilizó las mediciones de UFC/g de suelo obtenidos de cada tratamiento en la
fase experimental, graficó y trató de ajustar a uno o más de los modelos
matemáticos tomando en cuenta los basamentos teóricos de los modelos, el ajuste
gráfico a la tendencia de los datos y la obtención de estimadores iniciales de
los parámetros. Trabajó con 32 series de datos confeccionadas en las
condiciones de las plantas definidas como total, sanas y enfermas y a su vez,
sobre estas condiciones se definieron series de diferentes longitudes: serie
completa y en dos fases, creciente y decreciente.
En
total se seleccionaron 82 modelos usando el software R-Project y se eligieron
los cinco mejores modelos matemáticos considerando tendencias gráficas, pruebas
de t y F realizadas por el software R-Project, coeficientes basados en
desviación entre estimados y observados y criterios de información. Las series
seleccionadas para este trabajo pueden verse mejor en la tabla 3 junto con los
nombres de los modelos para cada serie y los valores de los criterios de
información de estos tomados de Bandera y Pérez (2018).
Tabla
3.
Series
para modelar el comportamiento de R. solanacearum en el suelo bajo las
diferentes condiciones del estudio.
|
SERIE
|
LONGITUD
|
MODELO
|
AIC
|
BIC
|
logLik
|
R2adj
|
|
TOTAL
|
Completa
|
Función Racional
Cuadrática
|
32,278
|
36,261
|
-12,139
|
0,867
|
|
TRATAMIENTO
1
|
Total
|
Completa
|
Bilogístico
|
10,150
|
15,129
|
-0,075
|
0,710
|
|
TRATAMIENTO
2
|
Total
|
Completa
|
Función Racional
Cuadrática
|
29,948
|
33,931
|
-10,974
|
0,672
|
|
TRATAMIENTO
3
|
Total
|
Completa
|
Ricker
|
74,842
|
77,829
|
-34,421
|
0,833
|
|
TRATAMIENTO
4
|
Total
|
Completa
|
Función Cuadrática
|
12,648
|
16,631
|
-2,324
|
0,850
|
|
TRATAMIENTO
5
|
Total
|
Completa
|
Función Racional
Cuadrática
|
84,512
|
88,495
|
-38,613
|
0,765
|
|
|
|
|
|
|
|
|
|
Fuente: Lugo (2018).
Para
el análisis de los datos se hace uso del software R, específicamente la función
gam() para lo cual es necesario cargar el paquete mgcv de Wood
(2006). Esta función puede usar p-splines univariantes según lo propuesto por
Eilers y Marx (1996). En realidad, este paquete contiene dos funciones que
permiten utilizar P-splines: gam y gamm, la diferencia entre las dos es que la
segunda permite elegir el parámetro de suavizado mediante REML, mientras que la
primera es similar a la función escrita por Hastie y Tibshirani (1990), pero
permite utilizar splines de rango bajo, además de haber corregido los errores
que existían en el cálculo de la varianza de los parámetros y elige el
parámetro de suavizado mediante la validación cruzada generalizada (GCV por sus
siglas en inglés). En ambos casos se puede imponer un valor arbitrario para el
parámetro de suavizado sin que sea elegido por la propia función, elegir la
base a utilizar, según las ofrecidas por el paquete y se puede elegir el número
de nodos y el orden de la penalización. Los argumentos de la función GAM se
muestran en la tabla 4.
Tabla
4.
Argumentos
de la función GAM.
|
ARGUMENTO
|
DEFINICIÓN
|
|
s(x, bs = “ps”)
|
Término de suavidad.
|
|
k
|
Tamaño de la base, nunca debe ser menor que
el orden de la penalización.
|
|
bs
|
Tipo de base que se
utiliza.
|
|
m
|
orden de la base y de
la penalización. Si 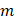 es un número único,
se toma como orden de base y orden de penalización es un número único,
se toma como orden de base y orden de penalización
|
|
by
|
Permite multiplicar
curvas por factores.
|
|
Nodos
|
Una lista que
contiene los nodos suministrados para la configuración básica, en el mismo
orden y con los mismos nombres que los datos. Este también puede ser nulo.
|
Fuente: Lugo (2018).
El procedimiento para analizar los datos en R
se hace de forma similar para las 6 series. Inicialmente se especifica un
modelo P spline a través de la función GAM con un término de suavizado de la
forma 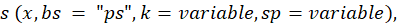 el
cual especifica una base P-spline con
el
cual especifica una base P-spline con 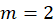 por
defecto, que significa una base y una penalización de segundo orden. “Las
diferencias entre los modelos dependerán de los argumentos variables como el
tamaño de base
por
defecto, que significa una base y una penalización de segundo orden. “Las
diferencias entre los modelos dependerán de los argumentos variables como el
tamaño de base 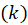 y el
parámetro de suavizado
y el
parámetro de suavizado 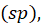 esto
con el fin de seleccionar el mejor ajuste p splines para los datos” (Burbano et
al., 2022, p. 270).
esto
con el fin de seleccionar el mejor ajuste p splines para los datos” (Burbano et
al., 2022, p. 270).
Es por ello que primero, se especifica un
modelo para la serie en cuestión variando el tamaño de base 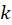 y se
hace una selección de los tres mejores modelos, dependiendo de los criterios de
información, métodos de selección del parámetro de suavizado e índices, los
cuales deben ser mínimos o máximos según sea el caso. Después de obtener el
mejor ajuste P spline, mediante un gráfico de dispersión, se verifica el efecto
del suavizado comparando este ajuste versus el modelo proporcionado por Lugo
(2018) como mejor para la descripción de la dinámica poblacional de R.
solanacearum en la serie especificada y se muestra la fórmula del modelo
aproximado para el mejor o los mejores ajuste P spline. Luego se cotejan las
curvas ajustadas para los distintos valores de
y se
hace una selección de los tres mejores modelos, dependiendo de los criterios de
información, métodos de selección del parámetro de suavizado e índices, los
cuales deben ser mínimos o máximos según sea el caso. Después de obtener el
mejor ajuste P spline, mediante un gráfico de dispersión, se verifica el efecto
del suavizado comparando este ajuste versus el modelo proporcionado por Lugo
(2018) como mejor para la descripción de la dinámica poblacional de R.
solanacearum en la serie especificada y se muestra la fórmula del modelo
aproximado para el mejor o los mejores ajuste P spline. Luego se cotejan las
curvas ajustadas para los distintos valores de 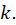
Segundo, al obtener el mejor ajuste en la parte
anterior, se procede a probar el mismo bajo diferentes valores de 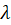 , con
el fin de obtener un valor de este parámetro que optimice el ajuste. Para
realizar la variación de λ, se toma como mínimo y máximo, aquel valor donde el
AIC tienda a aumentar. Para esto, se consideran los mismos ítems
que en la parte anterior. Seguidamente, sobre este
ajuste se contrasta gráficamente el efecto de distintos valores del parámetro
de suavizado. Los ítems que resumen la información arrojada por los tres
mejores modelos seleccionados para escoger el modelo final se describen en la
tabla 5.
, con
el fin de obtener un valor de este parámetro que optimice el ajuste. Para
realizar la variación de λ, se toma como mínimo y máximo, aquel valor donde el
AIC tienda a aumentar. Para esto, se consideran los mismos ítems
que en la parte anterior. Seguidamente, sobre este
ajuste se contrasta gráficamente el efecto de distintos valores del parámetro
de suavizado. Los ítems que resumen la información arrojada por los tres
mejores modelos seleccionados para escoger el modelo final se describen en la
tabla 5.
Tabla 5.
Ítems a
considerar para la selección del modelo final.
|
Ítem
|
Descripción
|
|
Modelo
|
Contiene
el nombre del modelo construido a partir de la siguiente nomenclatura, 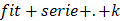 , por ejemplo, , por ejemplo, 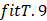 especifica un ajuste
p spline de la serie total con un tamaño de base k=9. Cuando el parámetro de
suavizado, especifica un ajuste
p spline de la serie total con un tamaño de base k=9. Cuando el parámetro de
suavizado, 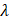 , es variable toma la
forma , es variable toma la
forma 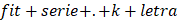 , para el modelo
anterior y la primera variación de , para el modelo
anterior y la primera variación de 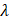 queda expresado de
la siguiente manera queda expresado de
la siguiente manera 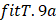 . .
|
|
Fórmula
|
Función
GAM del modelo.
|
|
Sp
|
Valor
del parámetro de suavizado estimado por la función GAM.
|
|
s(t)
|
Significación
aproximada del término de suavizado.
|
|
GCV
|
Valor
del método de selección del parámetro de suavizado, en este caso, Validación
Cruzada Generalizada.
|
|
AIC
|
Valor
del criterio de información de Akaike.
|
|
BIC
|
Valor
del criterio de información bayesiano.
|
|
LogLik
|
Valor
del logaritmo de la función de verosimilitud.
|
Fuente: Lugo (2018).
RESULTADOS
Los resultados se muestran para cada serie. Para efectos de
la comparación del método de suavizado P splines se usan los modelos de la
dinámica poblacional de R. solanacearum en el suelo obtenidos por Lugo
(2018) y que son etiquetados: modelototal para serie TOTAL, modeloT1 para serie
T1, modeloT2 para serie T2 y modeloT3. Cabe destacar, que la variable t, cuyos
datos corresponden a la columna DIA de la tabla 1, denota el intervalo de
tiempo en que se tomaron las mediciones de la variable respuesta y 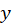 es
utilizada como variable predictora para modelar el ajuste en todas las series.
es
utilizada como variable predictora para modelar el ajuste en todas las series.
Se
presenta el modelo planteado por Lugo (2018) para describir la dinámica
poblacional de Ralstonia solanacearum en el suelo para la serie TOTAL:
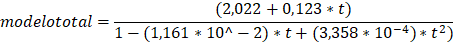
En
la tabla 6, se resumen los resultados obtenidos donde se puede observar que en
los tres ajustes P splines, el término de suavizado (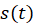 ),
resulta significativo. El modelo fitT.7 arrojó el menor GCV y BIC, sin embargo,
el ajuste denotado por el modelo fitT.9, presenta como favorables, tres de los
cinco criterios considerados para la selección del mejor, a saber, el menor AIC
y el mayor logLik y R2adj, por lo cual se considera como el modelo
con mejor ajuste y el modelo aproximado es el siguiente:
),
resulta significativo. El modelo fitT.7 arrojó el menor GCV y BIC, sin embargo,
el ajuste denotado por el modelo fitT.9, presenta como favorables, tres de los
cinco criterios considerados para la selección del mejor, a saber, el menor AIC
y el mayor logLik y R2adj, por lo cual se considera como el modelo
con mejor ajuste y el modelo aproximado es el siguiente:
fitT.9<-gam
(y ~ s(t, bs="ps",k=9))
Tabla 6.
Selección del mejor
ajuste P spline en serie TOTAL.
|
Modelo
|
Fórmula
|
Sp
|
s(t)
|
GCV
|
AIC
|
BIC
|
logLik
|
R2adj
|
|
fitT.7
|
(y
~ s (t, bs="ps”, k=7))
|
0,0726
|
5,86e-10
***
|
0,3285
|
35,0464
|
40,9273
|
-11,617
|
0,864
|
|
fitT.9
|
(y
~ s (t, bs="ps”, k=9))
|
0,3635
|
1,35e-09
***
|
0,3329
|
34,8921
|
41,3718
|
-10,939
|
0,868
|
|
fitT.11
|
(y
~ s (t, bs="ps”, k=11))
|
1,7761
|
2,2e-09
***
|
0,3355
|
35,0862
|
41,5134
|
-11,088
|
0,867
|
|
modelototal
|
función
racional cuadrática
|
|
|
|
32,278
|
36,261
|
-12,139
|
0,867
|
Fuente: Lugo (2018).
Se
representa las variantes del ajuste P spline. Note que los ajustes no son tan
distintos. En azul, el mejor ajuste. No obstante, al comparar con modelo total,
se evidencia que este presenta un menor AIC y un menor BIC en comparación con
el mejor ajuste P spline (Figura 1).
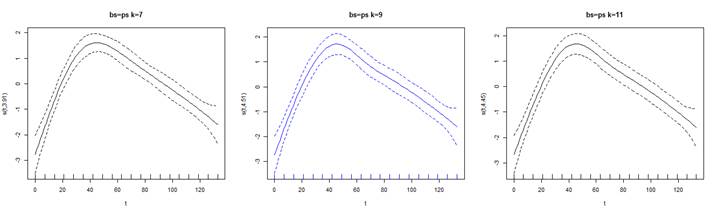
Figura 1. Representación gráfica
del efecto del suavizado con IC del 95% y 3 valores de k para la serie TOTAL.
Elaboración: El autor.
En
la figura 2, se contrasta el mejor ajuste P spline seleccionado versus modelo
total y puede verse que los modelos no difieren mucho, sin embargo, se nota
como el ajuste P spline genera una ondulación en la segunda mitad de los datos.
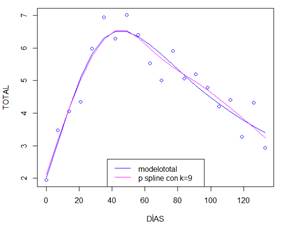
Figura 2. Mejor ajuste P spline
vs. modelo total.
Elaboración: El autor.
Ahora
bien, en el modelo seleccionado como mejor, fitT.9, se prueban cinco valores
distintos para λ entre 0,01 y 10, para un valor fuera de este rango el valor
del AIC tiende al aumento. En la tabla 7 se resume la
información arrojada. Tome en cuenta que el modelo fitT.9c
contiene un valor de 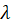 estimado
por la función GAM, este tiende a ser pequeño, lo que indica que se
está frente a un ajuste P splines.
estimado
por la función GAM, este tiende a ser pequeño, lo que indica que se
está frente a un ajuste P splines.
Tabla 7.
Selección de sp óptimo
sobre el mejor ajuste P spline en serie TOTAL.
|
Modelo
|
Fórmula
|
s(t)
|
GCV
|
AIC
|
BIC
|
logLik
|
R2adj
|
|
fitT.9a
|
(y
~ s (t, bs="ps”, k=9, sp=0,01))
|
1,61e-08 ***
|
0,3685
|
34,4565
|
43,3457
|
-8,3010
|
0,878
|
|
fitT.9b
|
(y
~ s (t, bs="ps”, k=9, sp=0,1))
|
1,64e-09 ***
|
0,3381
|
34,4225
|
41,8142
|
-9,7879
|
0,875
|
|
fitT.9c
|
(y
~ s (t, bs="ps”, k=9, sp=0,36))
|
1,36e-09 ***
|
0,3329
|
34,8867
|
41,3734
|
-10,9289
|
0,868
|
|
fitT.9d
|
(y
~ s (t, bs="ps”, k=9, sp=10))
|
2,88e-06 ***
|
0,5439
|
45,9348
|
50,2944
|
-18,5891
|
0,753
|
Elaboración: El autor.
Al
hacer las comparaciones, se encuentra que los modelos fitT.9a y fitT.9c presentan
igual número de criterios favorables para optimizar el ajuste. Los modelos
aproximados son:
presentan
igual número de criterios favorables para optimizar el ajuste. Los modelos
aproximados son:
fitT.9a<-gam
(y ~ s(t, bs="ps",k=9,sp=0,01)) y fitT.9c<-gam(y ~
(t,bs="ps",k=9,sp=0,36))
Cuando
la penalidad es más débil se obtiene una curva más ondulada, caso contrario
ocurre para un mayor 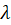 que
produce curvas más suaves. Esto puede verse mejor en la figura 3. A la
izquierda y en azul, el menor valor de
que
produce curvas más suaves. Esto puede verse mejor en la figura 3. A la
izquierda y en azul, el menor valor de 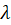 genera
una curva con más picos, en el centro, el modelo con
genera
una curva con más picos, en el centro, el modelo con 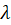 estimado
por la función GAM y a la derecha un
estimado
por la función GAM y a la derecha un 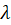 mayor.
mayor.
En
la figura 4 se evidencia de mejor forma como el valor de 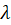 controla
la suavidad de la curva. Note la ondulación de la curva cuando
controla
la suavidad de la curva. Note la ondulación de la curva cuando 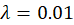 y la
tendencia lineal que toma cuando
y la
tendencia lineal que toma cuando 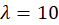 .
.
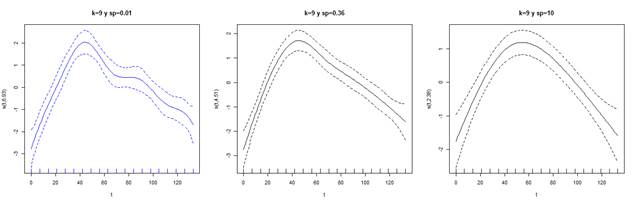
Figura 3. Mejor ajuste P spline
para 3 valores distintos de sp en serie TOTAL.
Elaboración: El autor.
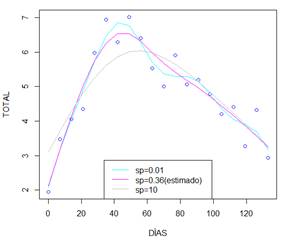
Figura 4. Efecto de sp sobre el
mejor ajuste P spline en serie TOTAL.
Elaboración: El autor.
Resultados de Serie T1
El
modelo planteado por Lugo (2018) para la serie T1, es el siguiente:
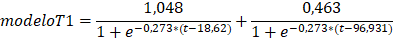
La
tabla 8, contiene los resultados para esta serie, donde se evidencia que los
tres modelos presentan un suavizado, s(t), significativo, no obstante, el
modelo fitT1.19, arrojó los menores valores para CGV, AIC, BIC y los mayores
valores para logLik y R2adj en comparación con los modelos restantes
y modeloT1, por lo que es considerado como el mejor modelo para el ajuste de
esta serie y el modelo aproximado es el siguiente:
FitT1.19<-gam
(y ~ s(t,bs="ps",k=19))
Tabla 8.
Selección del mejor
ajuste P spline para serie T1.
|
Modelo
|
Fórmula
|
Sp
|
s(t)
|
GCV
|
AIC
|
BIC
|
logLik
|
R2adj
|
|
fitT1.9
|
(y ~ s (t, bs="ps”, k=9))
|
0,2314
|
0,000208 ***
|
0,0962
|
9,8139
|
16,618
|
1,9265
|
0,717
|
|
fitT1.19
|
(y ~ s (t, bs="ps”, k=19))
|
0,0201
|
0,000739 ***
|
0,0560
|
-33,590
|
-16,386
|
34,0734
|
0,957
|
|
fitT1.20
|
(y ~ s (t, bs="ps”, k=20))
|
26,831
|
0,000358 ***
|
0,0984
|
9,9291
|
17,103
|
2,2394
|
0,718
|
|
modeloT1
|
Bilogístico
|
|
|
|
10,150
|
15,129
|
-0,075
|
0,710
|
Elaboración: El autor.
Visualice
en la figura 5 como cambia la curva para distintos valores de k. Es fácil notar
en el centro y en azul como el ajuste presenta una ondulación mayor en la curva
en comparación con los demás que producen curvas más suaves.
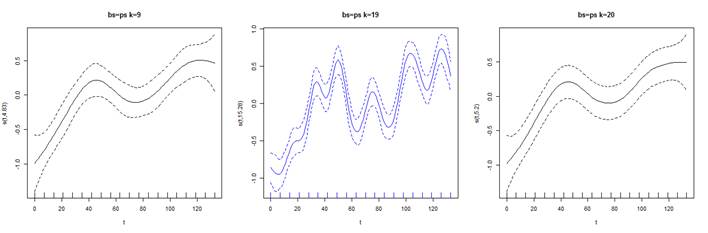
Figura 5. Representación gráfica
del efecto del suavizado con IC del 95% y 3 valores de k para la serie T1.
Elaboración: El autor.
En
la figura 6, se puede apreciar la diferencia entre las curvas que producen el
mejor ajuste P splines y modeloT1.
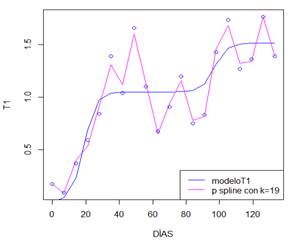
Figura 6. Mejor ajuste P spline
vs. modeloT1.
Elaboración: El autor.
En
la tabla 9 se encuentran los resultados para el control del suavizado del
ajuste, con un rango de variación de 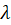 entre
0,00001 y 10. El modelo fitT1.19a presenta los menores valores de los criterios
de selección, sin embargo, este suavizado no es significativo. El modelo
fitT1.19c arrojó el menor GCV, pero el modelo fitT1.19b generó el menor AIC y
BIC y los mayores valores de logLik y R2adj, para el mejor ajuste de
la serie T1, aunque la incertidumbre aumenta en los extremos. El modelo
aproximado anterior es:
entre
0,00001 y 10. El modelo fitT1.19a presenta los menores valores de los criterios
de selección, sin embargo, este suavizado no es significativo. El modelo
fitT1.19c arrojó el menor GCV, pero el modelo fitT1.19b generó el menor AIC y
BIC y los mayores valores de logLik y R2adj, para el mejor ajuste de
la serie T1, aunque la incertidumbre aumenta en los extremos. El modelo
aproximado anterior es:
fitT.19b<-gam (y ~
s(t,bs="ps",k=19,sp=0,00001))
Tabla 9.
Selección de sp óptimo
para el mejor ajuste P spline en serie T1.
|
Modelo
|
Fórmula
|
s(t)
|
GCV
|
AIC
|
BIC
|
logLik
|
R2adj
|
|
fitT1.19a
|
(y ~ s
(t, bs="ps”, k=9, sp=1e-5))
|
0,128
|
0,1363
|
-62,845
|
-42,933
|
51,420
|
0,972
|
|
fitT1.19b
|
(y ~ s
(t, bs="ps”, k=9, sp=1e-4))
|
0,0841.
|
0,0978
|
-62,518
|
-42,806
|
51,055
|
0,975
|
|
fitT1.19c
|
(y
~ s (t, bs="ps”, k=9, sp=0,02))
|
0,00074
***
|
0,0560
|
-33,594
|
-16,389
|
34,075
|
0,957
|
|
fitT1.19d
|
(y
~ s (t, bs="ps”, k=9, sp=10))
|
0,000574
***
|
0,1016
|
9,6835
|
17,739
|
3,2491
|
0,728
|
Elaboración: El autor.
En
la figura 7, puede observarse el efecto de tres valores distintos de 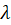 sobre
el mejor ajuste P spline.
sobre
el mejor ajuste P spline.
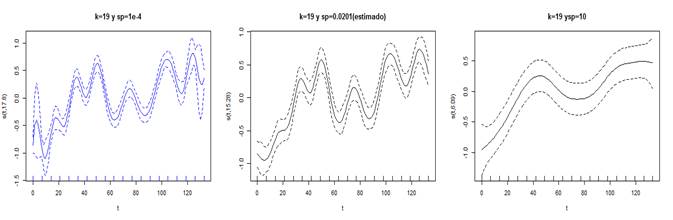
Figura 7. Mejor ajuste P spline
para 3 valores distintos de sp en serie T1.
Elaboración: El autor.
La figura 8, permite
comparar las curvas generadas por los ajustes P splines con los valores de 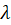 fijados
arbitrariamente y el estimado por la función GAM.
fijados
arbitrariamente y el estimado por la función GAM.
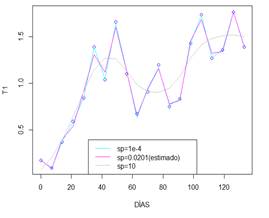
Figura 8. Efecto de sp sobre el
mejor ajuste P spline en serie T1.
Elaboración: El autor.
El
modelo sugerido por Lugo (2017) para la serie T2, es el siguiente:
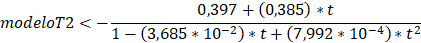
El
modelo anterior, no describe de forma correcta el patrón de datos
correspondiente, lo cual puede deberse a un error de transcripción. Por lo
anterior, el modelo aproximado se muestra a continuación:
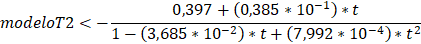
La
tabla 10, recoge los resultados arrojados por los modelos P splines planteados
para esta serie. Se puede ver que el modeloT1 presenta el menor BIC mientras
que el modelo fitT2.8 generó el menor GCV y AIC y el mayor logLik y R2adj,
así se considera a este modelo como la mejor aproximación para la serie T2 y su
modelo aproximado es el siguiente: fitT2.8<-gam (y
~ s(t, bs="ps",k=8))
Tabla 10.
Selección del mejor
ajuste P spline para serie T2.
|
Modelo
|
Modelo
|
sp
|
s(t)
|
GCV
|
AIC
|
BIC
|
logLik
|
R2adj
|
|
fitT2.7
|
(y
~ s (t, bs="ps”, k=7))
|
0,0449
|
0,000426
***
|
0,2674
|
30,7729
|
36,891
|
-9,2419
|
0,672
|
|
fitT2.8
|
(y
~ s (t, bs="ps”, k=8))
|
0,1787
|
0,000368
***
|
0,2671
|
30,6798
|
36,896
|
-9,0976
|
0,674
|
|
fitT2.9
|
(y
~ s (t, bs="ps”, k=9))
|
0,5286
|
0,000597
***
|
0,2716
|
31,0169
|
37,227
|
-9,2713
|
0,668
|
|
modeloT2
|
función
racional cuadrática
|
|
|
|
29,948
|
33,931
|
-10,974
|
0,672
|
Elaboración: El autor.
La
figura 9, permite contrastar los ajustes P splines para distintos valores de k.
En el centro y en azul la mejor aproximación. Note la ondulación que presenta
la curva en el extremo derecho y que los dos ajustes restantes no generan.
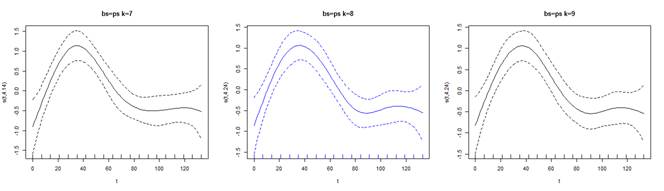
Figura 9. Representación gráfica
del efecto del suavizado con IC del 95% y 3 valores de k para la serie T2.
Elaboración: El autor.
Para
verificar la significancia del suavizado P splines en los datos, observe la
figura 10, donde se contrastan las curvas generadas por el mejor ajuste P
spline y modeloT2.
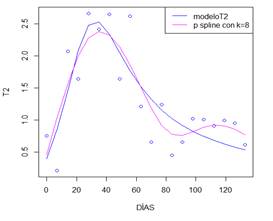
Figura 10. Mejor ajuste P spline
vs. modeloT2.
Elaboración: El autor.
Para
obtener el valor de 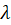 que
optimice el ajuste P spline, se varia en un rango entre 0.001 y 10. Sin
embargo, esta variación no causo un efecto significativo, ya que los criterios
de selección favorables son proporcionados por el modelo con el valor de
que
optimice el ajuste P spline, se varia en un rango entre 0.001 y 10. Sin
embargo, esta variación no causo un efecto significativo, ya que los criterios
de selección favorables son proporcionados por el modelo con el valor de 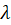 estimado
por la función GAM. El modelo fitT2.8a arrojó el mayor loglik, mientras que el
modelo fitT2.8c, con
estimado
por la función GAM. El modelo fitT2.8a arrojó el mayor loglik, mientras que el
modelo fitT2.8c, con 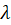 estimado,
presenta el menor GCV, AIC, BIC y el mayor R2adj. Estos resultados
se resumen en la tabla 11. El modelo aproximado para este ajuste es:
estimado,
presenta el menor GCV, AIC, BIC y el mayor R2adj. Estos resultados
se resumen en la tabla 11. El modelo aproximado para este ajuste es:
fitT2.8c<-gam (y ~ s (t, bs="ps",k=8,sp=0,178))
Tabla 11.
Selección de sp óptimo
para el mejor ajuste P spline en serie T2.
|
Modelo
|
Fórmula
|
s(t)
|
GCV
|
AIC
|
BIC
|
logLik
|
R2adj
|
|
fitT2.8ª
|
(y
~ s (t, bs="ps”, k=8, sp=1e-3))
|
0,0025 **
|
0,3469
|
33,392
|
42,173
|
-7,878
|
0,65
|
|
fitT2.8b
|
(y
~ s (t, bs="ps”, k=8, sp=0,01))
|
0,00124 **
|
0,3071
|
31,973
|
39,885
|
-8,039
|
0,669
|
|
fitT2.8c
|
(y
~ s (t, bs="ps”, k=8, sp=0,178))
|
0,000368 ***
|
0,2671
|
30,679
|
36,896
|
-9,098
|
0,674
|
|
|
fitT2.8d
|
(y
~ s (t, bs="ps”, k=8, sp=10))
|
0,0384 *
|
0,4735
|
43,303
|
47,292
|
-17,64
|
0,335
|
Elaboración: El autor.
La
figura 11, permite comparar los ajustes generados por las variaciones en 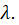 Las
curvas ajustadas no difieren una de la otra en mayor proporción, excepto la
curva con un
Las
curvas ajustadas no difieren una de la otra en mayor proporción, excepto la
curva con un 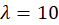 que
tiende a la linealidad. Aprecie esto de mejor forma en la figura 12.
que
tiende a la linealidad. Aprecie esto de mejor forma en la figura 12.
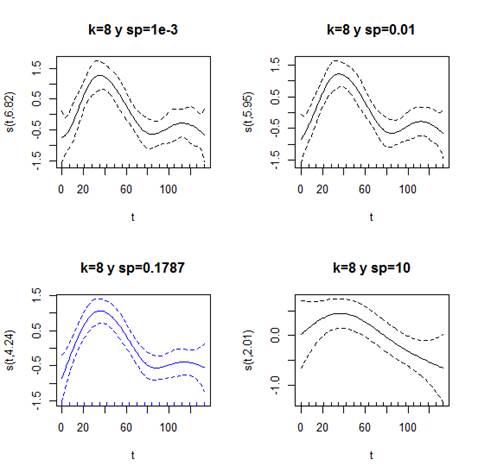
Figura 11. Mejor ajuste P spline
para 3 valores distintos de sp en serie T2.
Elaboración: El autor.
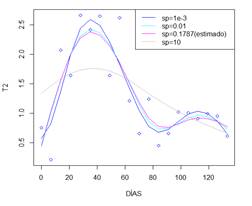
Figura 12. Efecto de sp sobre el
mejor ajuste P spline en serie T2.
Elaboración: El autor.
El
modelo a partir de los datos sugerido por Lugo (2017) para la serie T3 es:
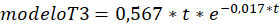
En
la tabla 11, se plasman los resultados obtenidos para los ajustes P splines. El
modeloT3 obtuvo el menor BIC mientras que el modelo fitT3.9 con arrojó el menor
GCV y AIC y el mayor logLik y R2adj. Así, el mejor modelo para
ajustar esta serie queda denotado por fitT3.9. el cual tiene la siguiente
forma: fitT3.9<-gam (y ~
s(t,bs="ps",k=9))
Tabla 11.
Selección del mejor
ajuste P spline para serie T3.
|
Modelo
|
Base
|
Sp
|
s(t)
|
GCV
|
AIC
|
BIC
|
LogLik
|
R2adj
|
|
fitT3.9
|
(y ~ s(t, bs="ps",k=9))
|
0,0074
|
4,57e-07 ***
|
2,6909
|
73,982
|
83,047
|
-27,887
|
0,856
|
|
fitT3.19
|
(y ~ s(t,bs="ps",k=19))
|
45,233
|
1,24e-06 ***
|
2,8766
|
78,131
|
84,463
|
-32,752
|
0,81
|
|
fitT3.20
|
(y ~ s(t,bs="ps",k=20))
|
57,273
|
1,2e-06 ***
|
2,8755
|
78,108
|
84,461
|
-32,673
|
0,811
|
|
modeloT3
|
Ricker
|
|
|
|
74,842
|
77,829
|
-34,421
|
0,833
|
Elaboración: El autor.
La
figura 13, muestra el efecto del suavizado en los datos para los distintos
valores de k utilizados para la serie T3. A la izquierda y en azul, el modelo
seleccionado como mejor ajuste P spline. Presenta una mayor ondulación. Se
aprecia, el efecto del suavizado en las curvas.
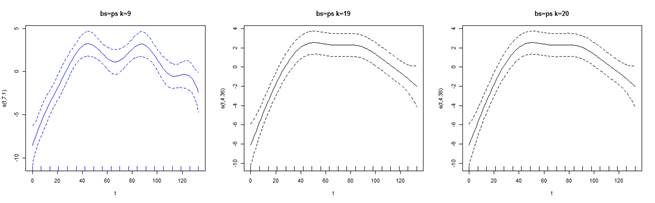
Figura 13. Representación gráfica
del efecto del suavizado con IC del 95% y 3 valores de k para la serie T3.
Elaboración: El autor.
En
la figura 14, se pueden cotejar las curvas generadas por el mejor ajuste P
splines en la serie T3 y modeloT3. El modelo P spline genera una curva menos
lineal.
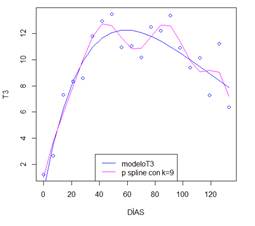
Figura 14. Mejor ajuste P spline
vs. modeloT3.
Elaboración: El autor.
La
tabla 12, resume los resultados arrojados para la selección del valor óptimo de
λ sobre el mejor ajuste P spline para la serie T3. El modelo fitT3.9a generó el
mayor logLik y R2adj, este último valor compartido con el modelo fitT3.9b que a
su vez obtuvo el menor AIC. Así mismo, el modelo fitT3.9c arrojó el menor GCV y
BIC. Cada uno de los modelos tienen dos criterios de selección a su favor, sin
embargo, se considera más relevante el valor del AIC, así se toma como mejor
ajuste al modelo denotado por fitT3.9b y su modelo aproximado es: fitT3.9b<-gam
(y ~ s(t,bs="ps",k=9,sp=0,0029))
Tabla 12.
Selección de sp óptimo
para el mejor ajuste P spline en serie T3.
|
Modelo
|
Fórmula
|
s(t)
|
GCV
|
AIC
|
BIC
|
LogLik
|
R2adj
|
|
fitT3.9ª
|
(y
~ s (t, bs="ps”, k=9, sp=0,001))
|
6,4e-07 ***
|
2,811
|
73,807
|
83,584
|
-27,084
|
0,859
|
|
fitT3.9b
|
(y
~ s (t, bs="ps”, k=9, sp=0,0029))
|
5,68e-07 ***
|
2,732
|
73,655
|
83,158
|
-27,283
|
0,859
|
|
fitT3.9c
|
(y
~ s (t, bs="ps”, k=9, sp=0,0074))
|
5,7e-07 ***
|
2,691
|
73,982
|
83,047
|
-27,887
|
0,856
|
|
fitT3.9d
|
(y
~ s (t, bs="ps”, k=9, sp=10))
|
1,3e-05 ***
|
3,369
|
82,407
|
86,767
|
-36,825
|
0,748
|
Elaboración: El autor.
En
la figura 15, pueden compararse estos ajuste y a su vez notarse como se
comportan las curvas ajustadas cuando 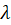 tiende
a aumentar, el ajuste se alisa más.
tiende
a aumentar, el ajuste se alisa más.
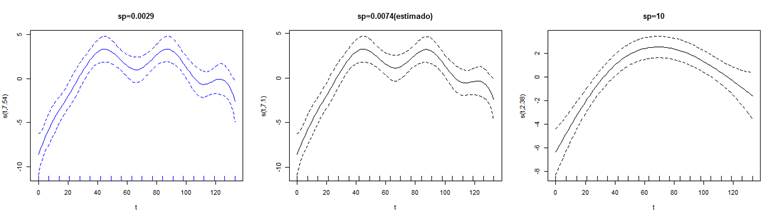
Figura 15. Mejor ajuste P spline
para 3 valores distintos de sp en serie T3.
Elaboración: El autor.
No
se aprecia mucha diferencia entre las curvas ajustadas de los modelos fitT3.9b
y fitT3.9c. Observe la figura 16 para identificar que el ajuste en las dos
curvas es casi idéntico.
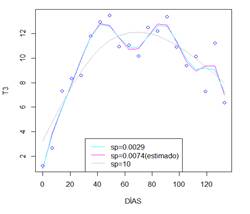
Figura 16. Efecto de sp sobre el
mejor ajuste P spline en serie T3.
Elaboración: El autor.
CONCLUSIONES
El
método P splines representa una herramienta muy útil en el suavizado de curvas
en presencia de datos no lineales. En la mayoría de las series analizadas,
proporcionó un ajuste satisfactorio, sin embargo, en algunos casos como series
Total y T4 que, aunque fueron significativos los ajustes, se consideran mejores
modelos los obtenidos por Lino (2017). En la búsqueda de un valor para 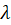 que
optimice el ajuste, se puede confiar en el estimado por la función GAM, ya que
proporcionó ajustes casi idénticos a los modelos con un valor de
que
optimice el ajuste, se puede confiar en el estimado por la función GAM, ya que
proporcionó ajustes casi idénticos a los modelos con un valor de 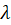 asignado que, de acuerdo con los criterios e índices considerados, fueron
seleccionados como modelo final.
asignado que, de acuerdo con los criterios e índices considerados, fueron
seleccionados como modelo final.
FINANCIAMIENTO
No monetario.
AGRADECIMIENTO
A todos los actores sociales involucrados
en el desarrollo de la investigación.
REFERENCIAS CONSULTADAS
Álvarez,
M, Grau, R, García, J, Quintana, R., y Cruz, A. (2015). Uso de técnicas
estadísticas para evaluar la rugosidad superficial en probetas de acero
inoxidable 316LVM sometidas a desgaste abrasivo comparativo. [Use of
statistical techniques to evaluate surface roughness in 316LVM stainless steel
specimens subjected to comparative abrasive wear]. Revista Técnica de la
Facultad de Ingeniería Universidad del Zulia, 38(1), 20-29. https://n9.cl/cig66
Bandera,
E., y Pérez, l. (2018). Los modelos lineales generalizados mixtos. Su
aplicación en el mejoramiento de plantas. [Generalized linear mixed models. Its
application in plant breeding] Cultivos Tropicales, 39(1),
127-133. https://n9.cl/v4vuu
Barrientos,
A., Olaya, J., y González, V. (2007). Un modelo spline para el pronóstico de la
demanda de energía eléctrica. [A spline model for forecasting electricity
demand] Revista Colombiana de Estadística, 30(2), 187-202. https://n9.cl/ctu86h
Burbano,
V., Valdivieso, M., y Burbano, Á. (2022). Modelos estadísticos no paramétricos
en los libros de texto del nivel universitario. [Non-parametric statistical
models in university-level textbooks] Revista de Investigación, Desarrollo e
Innovación, 12(2), 265-278. https://doi.org/10.19053/20278306.v12.n2.2022.15270
Durban,
R. (2009). Introducción al Suavizado con Penalizaciones: P-splines [An
introduction to smoothing with penalties:P-splines]. BEIO, Boletín de
Estadística e Investigación Operativa, 25(3), 195-205. https://n9.cl/2noir
Eilers,
P., y Marx, B. (1996). Suavizado Flexible con B-Splines y Penalizaciones. [Flexible
Smoothing with B-Splines and Penalties]. Statistical Science, 11(2),
89-102. https://n9.cl/ofjkyt
Hastie,
T., y Tibshiranri, R. (1990). Modelos aditivos generalizados. [Generalized
Additive Models]. https://n9.cl/0n7be
Lugo,
L. (2018). Efecto de bacterias antagonistas y extractos vegetales sobre la
dinámica poblacional de Ralstonia solanacearum (SMITH) YABUUCHI et al. Y la
expresión de síntomas en tomate (Solanum lycopersicum L.) [Effect of
antagonistic bacteria and plant extracts on the population dynamics of
Ralstonia solanacearum (SMITH) YABUUCHI et al. and the expression of symptoms
in tomato (Solanum lycopersicum L.] (Tesis doctoral). Doctorado en Ciencias
Agrícolas, Universidad Central de Venezuela, Maracay, Venezuela.https://n9.cl/utlmt
Ramírez,
A., y Polack, A. (2020). Estadística inferencial. Elección de una prueba
estadística no paramétrica en investigación científica. [Inferential
Statistics. Choice of a Non Parametric Statistical Test in Scientific Research]
Horizonte de la Ciencia, 10(19), 191-208. https://n9.cl/m9ybb
Salas,
E., Ojeda, N., y Soto, H. (2010). Métodos estadísticos paramétricos y no
paramétricos para predecir variables de rodal basados en Landsat ETM+: una
comparación en un bosque de Araucaria araucana en Chile. [Parametric
and nonparametric statistical methods for predicting stand variables based on
Landsat ETM+: a comparison in an Araucaria araucana forest in Chile]. Bosque, 31(3),179-194.
https://n9.cl/mxtppl
Toriz,
A., y Sánchez, A. (2017). Método de asociación de datos basado en curvas
B-Spline para el problema de SLAM en ambientes complejos. [Data
association method based on B-Spline curves for the SLAM problem in complex
environments]. Computación y Sistemas, 21(2),
353-368. https://doi.org/10.13053/cys-21-2-2724
Wood,
S. N. (2017). Modelos Aditivos Generalizados: Una Introducción. [Generalized
Additive Models: An Introduction]. (2nd ed.) Boca Raton, Fl, E.U.A: Chapman
Hall/CRC. https://n9.cl/l3yfy
©2024 por los autores.
Este artículo es de acceso abierto y distribuido según los términos y
condiciones de la licencia Creative Commons
Atribución-NoComercial-CompartirIgual 4.0 Internacional (CC BY-NC-SA 4.0) (https://creativecommons.org/licenses/by-nc-sa/4.0/).
![]() es el responsable de
controlar el suavizado y en la búsqueda de un valor para este parámetro que
optimice el ajuste, se puede confiar en el estimado por la función GAM, ya que
proporcionó ajustes casi idénticos a los modelos con un valor de
es el responsable de
controlar el suavizado y en la búsqueda de un valor para este parámetro que
optimice el ajuste, se puede confiar en el estimado por la función GAM, ya que
proporcionó ajustes casi idénticos a los modelos con un valor de ![]() asignado que de
acuerdo a los criterios e índices considerados, fueron seleccionados como
modelo final.
asignado que de
acuerdo a los criterios e índices considerados, fueron seleccionados como
modelo final.![]() consiste
en p+1 trozos de polinomios de grado
consiste
en p+1 trozos de polinomios de grado ![]() que
se unen en
que
se unen en ![]() nodos
internos (Salas et al., 2010).
nodos
internos (Salas et al., 2010).














