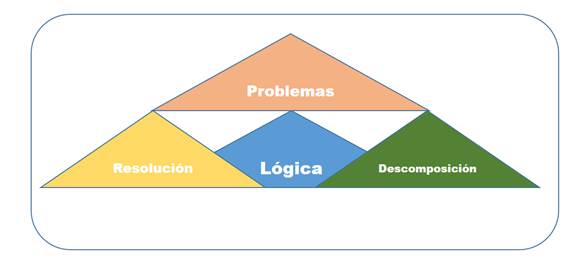
Figura 1. Lógica.
Elaboración: El autor.
La figura 1, describe la lógica aplicada en el área de la matemática, la cual constituye una técnica que permite a los niños descomponer y componer estructuras para la resolución de problemas relacionándolos con sus realidades.
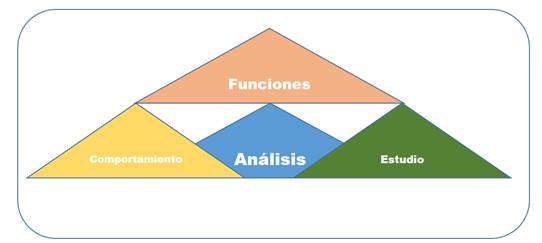
Figura 2. El análisis.
Elaboración: El autor.
La figura 2, muestra que el análisis es otra categoría derivada de la unidad de análisis habilidad del razonamiento matemático, la cual, según los docentes entrevistados, supone el estudio del comportamiento de las funciones. Por tanto, este aspecto debe ser abordado con los niños para contribuir a un aprendizaje óptimo en matemática.
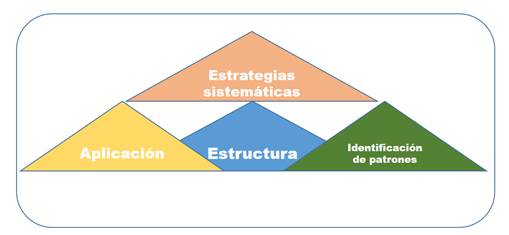
Figura 3. Estructura.
Elaboración: El autor.
La figura 3, explica que otro de los factores del razonamiento matemático lo constituye la estructura, la cual constituye la identificación de patrones y la aplicación de estrategias sistemáticas para la solución de problemas.
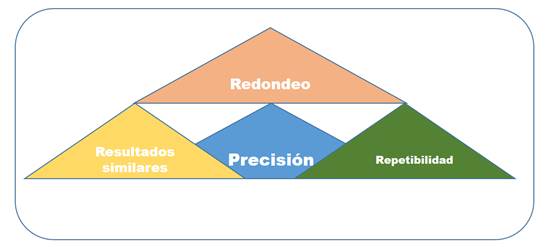
Figura 4. Precisión.
Elaboración: El autor.
La figura 4 revela que la precisión es otra de las categorías emergentes dentro de la habilidad de razonamiento matemático, ya que esta implica la repetibilidad, la obtención de resultados similares y el redondeo.
Figura 5. Creatividad.
Elaboración: El autor.
La figura 5, expone la categoría de la creatividad, la cual implica la resolución de soluciones novedosas, la búsqueda de diversos caminos y la originalidad al momento de solucionar problemas.
Por consiguiente, en cuanto al pensamiento variacional en la educación primaria, emergieron las siguientes categorías mostradas en las siguientes figuras.
Figura 6. Identificación y descripción.
Elaboración: El autor.
La figura 6 expone la categoría de identificación y descripción de patrones y magnitudes que varían, aspectos que deben ser considerados en la práctica de las matemáticas para facilitar el progreso de los estudiantes de primaria. Lenz (2022) apoya la praxis del pensamiento relacional para facilitar el aprendizaje de las matemáticas al integrar las expresiones matemáticas y las ecuaciones como un todo mediante el empleo de materiales reales, lo que les condujo a resolver cantidades interdependientes.
Figura 7. Uso de gráficos.
Elaboración: El autor.
En la figura 7, se evidencia el uso de gráficos como otra de las categorías emergentes, los cuales se basan en la representación y visualización de conceptos abstractos, por tanto, deben ser tomados en cuenta, ya que según Sterner (2024), estos ayudan al desarrollo del pensamiento funcional de los estudiantes a través de la generalización de patrones y la interacción con conversaciones de pensamiento covariacional.
Figura 8. Uso de variables y patrones.
Elaboración: El autor.
En la figura 8, se muestra la categoría relacionada con el uso de variables y patrones, los cuales se fundamentan en la configuración de situaciones dinámicas motivacionales. Esto es cónsono con el estudio de Vera et al. (2024), quienes sugieren el empleo de estrategias motivacionales para la participación en la solución de problemas contextualizados en la realidad áulica.
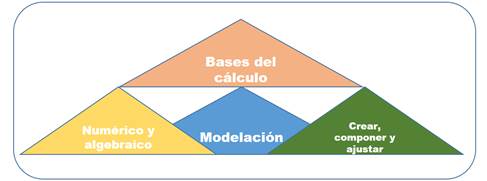
Figura 9. Modelación.
Elaboración: El autor.
La figura 9, se basa en la categoría modelación, la cual supone la creación, composición, ajuste y conexión de lo numérico con lo algebraico, aspectos importantes para sentar las bases del cálculo en la educación primaria.
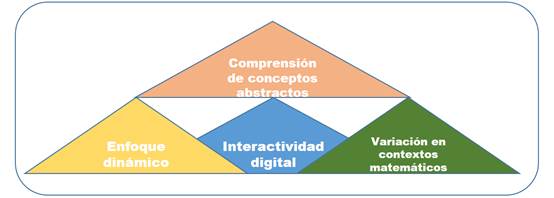
Figura 10. Interactividad digital.
Elaboración: El autor.
La figura 10, describe la categoría de la interactividad digital, la cual se basa en el análisis de la variación en los contextos matemáticos, pasando de un enfoque estático a uno dinámico, mediante el empleo de las TIC, facilitando así la comprensión de fórmulas, de cálculos y de conceptos abstractos. Suárez et al. (2022) afirman que el pensamiento variacional se puede desarrollar desde el nivel de primaria mediante diversas intervenciones pedagógicas. Por tanto, acudir a las TIC constituye una alternativa clave para el desarrollo de dicho pensamiento.
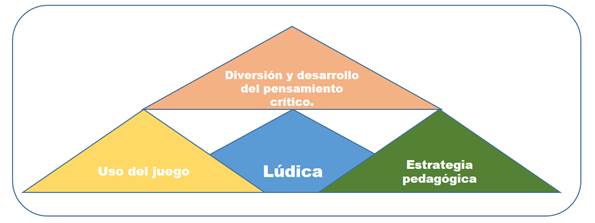
Figura 11. Lúdica.
Elaboración: El autor.
La figura 11, revela que la lúdica se resalta como una estrategia pedagógica sustentada en el empleo del juego, a fin de lograr la diversión de los niños y el desarrollo del pensamiento crítico dentro del área de matemática. En este respecto, Guevara et al (2023) afirman que la gamificación influye de forma positiva en el aprendizaje de las matemáticas en niños de primaria.
Por último, la figura 12, muestra que, para lograr un aprendizaje significativo en la práctica de las matemáticas a nivel de primaria, se debe lograr la autonomía estudiantil, ya que esta supone la capacidad para resolver problemas por sí mismos.
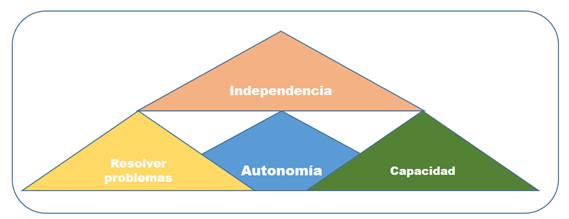
Figura 12. Autonomía.
Elaboración: El autor.
DISCUSIÓN
Al inicio del estudio, se pudo apreciar que experiencias previas ratifican que el aprendizaje de las matemáticas constituye un proceso complejo, sobre todo, a nivel de primaria. Sin embargo, este estudio ha permitido confirmar que cuando los entes gubernamentales, las instituciones educativas, los docentes y la familia se unen, se puede lograr una optimización de la enseñanza. En este particular, Naranjo (2024) expresa que las estrategias matemáticas contribuyen al fomento de la creatividad, del pensamiento crítico y de la innovación escolar. Al respecto, Infante et al. (2025) manifiestan que el factor para el desarrollo del pensamiento crítico lo constituye la dialógica. Por ende, los docentes deben propiciar un ambiente de aprendizaje en el cual interactúen con los estudiantes para crear un clima de confianza que facilite la comprensión de cada contenido.
Abel et al. (2022) proponen la inclusión de las TIC en el proceso de instrucción en el aula; por ende, es importante desarrollar programas de formación constante que conduzcan a los docentes hacia la optimización del aprendizaje de las matemáticas en los estudiantes, especialmente en los niños, desde un enfoque activo.
En este mismo orden de ideas, De Vera y Balgua (2023) manifiestan que el uso de herramientas tecnológicas facilita el aprendizaje de las matemáticas. Por su parte, Engelbrecht y Borba (2024) apoyan la aseveración de los autores anteriores al afirmar que las TIC intervienen de forma positiva en el aprendizaje de las matemáticas.
Ello también conduce a afirmar que el empleo de la lúdica constituye una acción motivadora para la práctica de la matemática, ya que se basa en una estrategia pedagógica que permite el logro de un aprendizaje significativo mediante la diversión y el desarrollo del pensamiento crítico.
Se pudo apreciar mediante las entrevistas que, la habilidad del razonamiento matemático incluye aspectos como el desarrollo de la lógica, el análisis, la estructura, la precisión y la creatividad. Por otro lado, el pensamiento variacional implica el alcance de la autonomía y de la comprensión de la matemática mediante el uso de gráficos, patrones, la lúdica, entre otros los cuales giraron en torno a un progreso estudiantil enfocado en la educación primaria.
Por último, es menester destacar que, pensar en el aprendizaje de la matemática no es algo elemental, sino que, por el contrario, va más allá de la simple comprensión de números, siendo un factor necesario para la vida; por tanto, su práctica en el nivel de primaria contribuye con la preparación de los estudiantes para los siguientes niveles de la educación. Esta aseveración coincide con la apreciación de Rivera et al. (2023), quienes expresan que la educación tiene como objetivo formar a los aprendices con las habilidades clave para enfrentarse a su futuro.
CONCLUSIONES
A manera de conclusión, se puede expresar que, para lograr un proceso de formación óptimo en el área de matemática, los docentes deben aplicar estrategias variadas y motivadoras que despierten los intereses de los niños de primaria hacia la práctica esta.
Asimismo, los entes gubernamentales, el personal de las instituciones educativas y la familia deben unir esfuerzos para desarrollar un currículo sustentado en el desarrollo de la habilidad del razonamiento matemático desde el pensamiento variacional, considerando la lúdica como una de las estrategias pedagógicas clave.
Según las opiniones de los docentes, aspectos como la lógica, la precisión, la creatividad, entre otros integran la habilidad del razonamiento matemático y factores como el uso de gráficos, de los juegos, de la interactividad mediante las TIC, promueven la autonomía y el desarrollo del pensamiento crítico.
Finalmente, no se puede obviar que todos los elementos antes mencionados han contribuido con el desarrollo de las habilidades matemáticas en los estudiantes de primaria, siendo fundamental para su futuro como estudiantes de secundaria y a futuro, del nivel universitario.
FINANCIAMIENTO
No monetario.
AGRADECIMIENTO
Gracias a los docentes informantes clave por sus valiosos aportes al desarrollo del presente recorrido investigativo.
REFERENCIAS CONSULTADAS
Abel, V., Tondeur, J., & Sang, G. (2022). Teacher perceptions about ICT integration into classroom instruction. Education Sciences, 12(9), 609. https://n9.cl/fnziog
De Vera, M., y Balgua, B. (2023). Utilization of technologies in teaching mathematics in a flexible learning environment. In International Conference on Information Technology and Mechatronics Engineering (Icitme), 2602(1), 030004. https://n9.cl/9z3wj
Engelbrecht, J., & Borba, M. C. (2024). Recent developments in using digital technology in mathematics education. ZDM–Mathematics Education, 56(2), 281-292. https://n9.cl/ajlef9
Guevara, G., Madariaga, L., Reyes, C., y Zuleta, C. (2023). Gamificación para el desarrollo del aprendizaje de las operaciones matemáticas en tercero básico. Información tecnológica, 34(4), 31-44. https://n9.cl/h4l0r
Infante, M., Isea, J., y Méndez, C. (2025). Building critical thinking from dialogical praxis in the university classroom. Revista Conrado, 21(105), e 4697. https://n9.cl/ab0rj
Isea, J., Molina, T., Álvarez, G., y Romero, A. (2025). Impact of academic stress on the well-being of postgraduate students: coping Strategies. Salud, Ciencia y Tecnología - Serie de Conferencias, 4, 628. https://n9.cl/suqky
Lenz, D. (2022). The role of variables in relational thinking: an interview study with kindergarten and primary school children. ZDM–Mathematics Education, 54(6), 1181-1197. https://n9.cl/4f1tq
Molina, T., Lizcano, C., Burbano, L., e Isea, J. (2025). Discurso metacomunicativo como herramienta para el aprendizaje en el aula. Metacommunicative discourse as a tool for learning in the classroom. Revista Conrado, 21(103), e4353. https://n9.cl/30pax
Naranjo-Mora, M. (2024). Estrategias matemáticas, desarrollo sostenible y su incidencia en estudiantes de bachillerato. Cienciamatria. Revista Interdisciplinaria de Humanidades, Educación, Ciencia y Tecnología, 10(18), 275-288. https://n9.cl/5fmsrz
Oktaviani, W., Herman, T., & Darhim, D. (2022). Didactic design to improve mathematical reasoning ability of high school students on derivative application materials. In AIP Conference Proceedings, 2577(1), 020047. https://n9.cl/uyunn
Ríos, P., Duran, K., y Mucha, L. (2025). Actividades lúdicas para mejorar habilidades numéricas en estudiantes educación básica regular. EPISTEME KOINONIA, 8(1), 177-190. https://n9.cl/gh0ipa
Rivera, G., Lera, L., Poleo, A., Rivera, A., y von Feigenblatt, O. (2023). El liderazgo educativo en los programas de educación especial: Una revisión de la literatura. Anales de la Real Academia de Doctores de España, 8(4), 85-801. https://n9.cl/wlkzfd
Sterner, H. (2024). Using graphical representations to develop students’ correspondence relationships and covariational thinking in pattern generalizations in primary school. International Journal of Science and Mathematics Education, 1-25. https://n9.cl/xb20yr
Suárez, C. A. H., Castro, W. R. A., y Suárez, A. A. G. (2022). Development of variational thinking based on non-routine problem-solving in elementary school students. Journal of Language and Linguistic Studies, 18(2). https://n9.cl/2hlrh
Vera, M., Mendoza, A., y Beltrán, L. (2024). Intervención de la motivación docente en el logro de los objetivos de aprendizaje: Percepción de los docentes. Revista gestión de las personas y tecnología, 17(20), 1-20. https://n9.cl/7dx0p
©2026 por el autor. Este artículo es de acceso abierto y distribuido según los términos y condiciones de la licencia Creative Commons Atribución-NoComercial-CompartirIgual 4.0 Internacional (CC BY-NC-SA 4.0) (https://creativecommons.org/licenses/by-nc-sa/4.0/).