https://doi.org/10.35381/e.k.v8i2.4857
Estrategias para mejorar los procesos inferenciales en la resolución de problemas matemáticos: Una revisión sistemática
Strategies for improving inferential processes in mathematical problem solving: a systematic review
Maira Lucía Castillo-Álvarez
Universidad César Vallejo, Trujillo, Trujillo
Perú
https://orcid.org/0000-0002-0824-7329
Kony Luby Durán-Llaro
Universidad César Vallejo, Trujillo, Trujillo
Perú
https://orcid.org/0000-0003-4825-3683
Revisado: 25 de septiembre 2025
Aprobado: 15 de noviembre 2025
Publicado: 01 de diciembre 2025
RESUMEN
El artículo presentado tuvo como propósito analizar los procesos inferenciales en los aprendices cursantes de la educación secundaria en la resolución de problemas matemáticos. Como metodología, se llevó a cabo la revisión documental de 15 artículos correspondientes a Scopus, SciELO y Web of Science. Estos fueron seleccionados mediante el método PRISMA entre los años 2021 y 2025. Como resultado, se indicó que el empleo de las tecnologías y del enfoque cooperativo e interdisciplinario resultó ser efectivo para el aprendizaje. Asimismo, las estrategias de comprensión lectora constituyen las bases para la inferencia. Por tanto, se concluyó que estas alternativas educativas son viables para facilitar el aprendizaje de la matemática.
Descriptores: Estrategias didácticas; resolución de problemas; educación secundaria; proceso inferencial. (Tesauro UNESCO).
ABSTRACT
The purpose of this article was to analyze the inferential processes used by secondary school students in solving mathematical problems. The methodology consisted of a literature review of 15 articles from Scopus, SciELO, and Web of Science. These were selected using the PRISMA method between 2021 and 2025. The results indicated that the use of technology and a cooperative and interdisciplinary approach proved to be effective for learning. Likewise, reading comprehension strategies form the basis for inference. Therefore, it was concluded that these educational alternatives are viable for facilitating mathematics learning.
Descriptors: Teaching strategies; problem solving; secondary education; inferential process. (UNESCO Thesaurus).
INTRODUCCIÓN
La resolución de problemas matemáticos constituye una competencia esencial para lograr un aprendizaje integral en los estudiantes, ya que se precisa como una de las competencias principales en el ámbito educativo, especialmente en la Educación Básica Regular del nivel secundaria, donde los estudiantes resuelven sus problemas de forma presencial; no obstante, resolver una situación problemática sigue siendo un gran desafío cognitivo.
Si bien es cierto, los estudiantes primeramente leen el problema para buscar la alternativa de solución; no obstante, muchos de ellos muestran dificultades al comprenderlo y, por ende, al seleccionar los datos significativos que les permitan emplear el plan indicado para elegir el procedimiento adecuado.
Las habilidades en la resolución de problemas matemáticos trascienden el aula y se aplican a la vida cotidiana. Por tal motivo, el abordaje mecánico de procedimientos u otras capacidades pueden conectar la información y construir significados a partir de una información ya sea implícita o explícita. Los procesos inferenciales son un componente clave para desarrollar un pensamiento lógico matemático, ya que ayuda a establecer conexiones entre elementos de un problema y las estrategias necesarias para su solución (Dioses et al., 2024; Oktaviani et al. 2022). Esta capacidad no solo está relacionada con habilidades cognitivas y con la comprensión lectora, que actúa como mediadora entre el problema planteado y la estrategia de resolución seleccionada por el estudiante.
A este respecto, se considera relevante destacar algunas investigaciones que han demostrado ciertas dificultades que enfrentan los aprendices al momento de inferir para resolver los problemas matemáticos. Tales dificultades suelen deberse a sus limitantes formas de interpretar enunciados, de identificar datos significativos y de seleccionar las estrategias adecuadas. Para Oktaviani et al. (2022), un plan didáctico podría disminuir las deficiencias en los cálculos matemáticos, especialmente, en tareas que requieren un análisis profundo y lógico. Por consiguiente, es imprescindible fortalecer las destrezas numéricas en el hecho escolar de forma urgente.
En la educación secundaria, los aprendices tienden a experimentar una etapa crítica de su habilidad cognitiva, ejerciendo los procesos inferenciales gran influencia en las destrezas de orden superior como la inferencia, lo cual demanda un mayor esfuerzo para ello, la interacción social y el andamiaje surgen como alternativas para resolver los problemas de forma grupal (Infante et al., 2025).
De allí que, el diseño de planes de estrategias didácticas para el fomento del pensamiento crítico y lógico podría tener un impacto significativo en la capacidad de los estudiantes para comprender de forma lectora diversas situaciones. Para tal fin se sugiere la aplicación de actividades flexibles y creativas como las propuestas por (Rice y Wijekumar, 2024; Von Feigenblatt et al., 2022 y Munaji et al., 2025).
Desde otra perspectiva, la relación entre la comprensión lectora en el área de la matemática y los procesos inferenciales son dominadas por estudiantes con niveles avanzados; así lo establecen (Rice y Wijekumar, 2024). Ello señala que la enseñanza de las matemáticas debe abarcarse desde una visión interdisciplinaria. En esta misma línea, Boice et al. (2024) asevera que el análisis inferencial contribuye a mejorar el rendimiento de los estudiantes en los cálculos numéricos. Por esta razón, se hace necesaria la implementación de metodologías activas que fomenten un pensamiento crítico e inferencial en matemática (Infante et al., 2025).
A nivel global, es bien sabido que el razonamiento matemático ha llegado a ser parte de todos los currículos, lo cual ha generado interés por indagar esta área desde la instancia investigativa. En el ámbito nacional, las evaluaciones censales han reflejado un bajo rendimiento en matemática, por lo cual, es necesario investigar y aplicar estrategias para mejorar el desarrollo de los procesos inferenciales.
Con base en los anteriores planteamientos, la presente investigación tuvo como objetivo analizar los procesos inferenciales en los estudiantes de secundaria para la resolución de problemas matemáticos. Ante ello, se indagó acerca de las estrategias y los factores asociados a la mejora de los procesos inferenciales, planteando como meta el fomento de competencias matemáticas desde una visión holística, abriendo paso a todas las opciones pertinentes a la temática tratada (Litardo, 2023; Bhor y Varghese, 2024). Para resumir, el presente artículo busca el fortalecimiento de las habilidades matemáticas, considerando tanto las implicaciones pedagógicas como los factores contextuales que intervienen en el aprendizaje de las matemáticas.
MÉTODOS
El estudio se sustentó en un enfoque cualitativo de tipo documental, el cual permitió analizar una serie de artículos basados en los procesos inferenciales para la resolución de problemas matemáticos. Para la selección de los estudios, se consideró el método PRISMA. Tal elección, se dividió en 4 fases. En una primera fase, se realizó la búsqueda en Scopus, SciELO y Web of Science. Se precisaron términos de búsqueda específicos como: "Resolución de problemas matemáticos", “Procesos inferenciales”, "Educación secundaria", “Estrategias didácticas” y "Comprensión lectora inferencial". En esta etapa, se obtuvo un total de 30 investigaciones.
En la fase 2, se tomaron en cuenta los criterios de inclusión y exclusión, entre los cuales se incluyeron publicaciones teniendo en cuenta el idioma (español, inglés o portugués), estudios realizados entre 2021 y 2025 y artículos fundamentados en diversos enfoques, los cuales abarcaron directamente los procesos inferenciales y la resolución de problemas matemáticos. Por otro lado, se excluyeron 10 artículos por falta de relevancia, luego, 5 artículos fueron eliminados, ya que no cumplieron con los criterios de inclusión, pues no proporcionaron resultados claros y no aportaron aspectos significativos relacionados con los procesos inferenciales.
Luego de aplicar tales criterios, se eligieron 15 estudios considerados pertinentes para su revisión y análisis. En la tercera fase, los estudios seleccionados se analizaron cualitativamente para identificar sus coincidencias clave, teniendo en cuenta la técnica del análisis documental y empleándose un instrumento de registro elaborado para ordenar la información más importante. Las secciones que se incluyeron en el instrumento permitieron documentar aspectos como: autor, año, base de datos, título, implicaciones y la pertinencia de estos mediante la escala de Likert. En la última fase, se llevó a cabo un análisis cualitativo que permitió categorizar las estrategias didácticas implementadas y las principales dificultades enfrentadas por los estudiantes considerando los procesos inferenciales y la resolución de problemas matemáticos.
RESULTADOS
Los resultados del estudio, tal como se observa en la figura 1, resumen la importancia de los procesos inferenciales en cuanto a la resolución de problemas matemáticos.
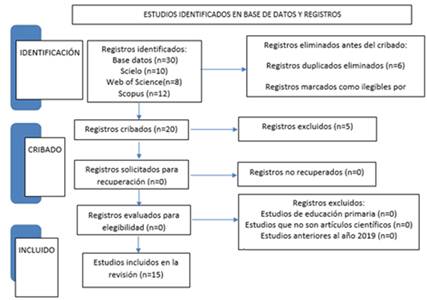
Figura 1. Diagrama de flujo prisma.
Elaboración: Los autores
En la etapa de identificación, se inició con un total de 30 estudios de las bases de datos: Scopus (12), SciELO (10) y Web of Science (8). Sin embargo, se eliminaron 6 artículos duplicados y 4 marcados como ilegibles por herramientas de automatización, un número significativo de registros. Durante la etapa del cribado, se analizaron 20 artículos, luego 5 fueron descartados por no cumplir los criterios de inclusión establecidos en la revisión, quedando finalmente, 15 artículos para su análisis. La figura 1 sintetiza los pasos antes descritos.
Cabe acotar que la base de datos Scopus y Web of Science resaltan como una fuente principal al contribuir con la mayoría de los artículos, mientras que SciELO aportó 6 estudios. Así mismo, se evidencian 6 artículos en español, 9 en inglés.
Como se observa en la tabla 1, entre los elementos clave, cada artículo incluyó entre sus variables los procesos inferenciales y la resolución de problemas matemáticos, así como las estrategias didácticas (Litardo, 2023), considerando los criterios de pertinencia de la escala de Likert.
Tabla 1.
Matriz de pertinencia de los estudios incluidos en la revisión sistemática.
|
ID |
Autor/año |
Título |
Implicaciones |
Escala de Likert |
|
||||
|
1 |
2 |
3 |
4 |
5 |
|||||
|
1 |
Dioses, L., Dios, M., y Sabino, C. (2024). SciELO. |
Programa de estrategias de resolución de problemas para fortalecer el pensamiento divergente en matemática en estudiantes de secundaria. |
Resolución de problemas matemáticos y mejoramiento de la comprensión de conceptos. |
|
|
|
|
x |
|
|
2 |
Gamarra, J., Duran, K., y Mucha, L. (2025). SciELO. |
Impacto de las estrategias motivacionales en la resolución de problemas matemáticos en primaria. |
La aplicación del método Singapur contribuyó a mejorar la resolución de problemas matemáticos. |
|
|
|
x |
|
|
|
3 |
Gorbalan, I., Duran, K., y Mucha, L. (2025). SciELO. |
Método Singapur para mejorar la resolución de problemas matemáticos en estudiantes de educación básica regular. |
Las estrategias innovadoras son herramientas clave para aumentar el interés y el desempeño de los estudiantes. |
|
|
|
|
x |
|
|
4 |
Litardo, A. (2023). SciELO. |
Las estrategias didácticas y el aprendizaje de las matemáticas en educación general básica. |
Mientras más innovadoras sean las estrategias, mayor será el interés de los estudiantes por aprender. |
|
|
|
x |
|
|
|
5 |
Orihuela, C. (2025). SciELO. |
Estrategias de resolución de problemas matemáticos en estudiantes: una revisión sistemática. |
Los profesores deben enfocarse en desarrollar estrategias para facilitar el aprendizaje de las matemáticas. |
|
|
|
x |
|
|
|
6 |
Orihuela, C. (2025). SciELO. |
Resolución de problemas y habilidades matemáticas en estudiantes de secundaria: Revisión sistemática. |
El desarrollo de habilidades matemáticas forma a los estudiantes para su vida. |
|
|
|
x |
|
|
|
7 |
Soledispa, G., y Parra, S. (2024). SciELO. |
Estrategias heurísticas en las capacidades de resolución de problemas matemáticos. |
La permanente aplicación de las estrategias heurísticas constituye un aporte en la solución de cálculos matemáticos. |
|
|
|
x |
|
|
|
8 |
Bhor, A., y Varghese, M. (2024). Scopus. |
Enseñanza basada en STEAM: Mejorando la calidad de la educación. |
Esta metodología basada en la Ciencia, la Tecnología, la Ingeniería, el Arte y las Matemáticas contribuye a mejorar la calidad educativa. |
|
|
x |
|
|
|
|
9 |
Boice, K., Alemdar, M., Jackson, J., Kessler, T., Choi, J., Grossman, S., y Usselman, M. (2024). Scopus/Web of Science. |
Explorando la comprensión y la implementación de STEAM por parte de los docentes: no hay una solución única para todos. |
Los profesores requieren apoyo en el empleo de la metodología para ajustarlos a cada área de enseñanza. |
|
|
x |
|
|
|
|
10 |
Molina, T., Lizcano, C, Burbano, L., y Isea, J. (2025). SciELO. |
Discurso meta-comunicativo como herramienta para el aprendizaje en el aula. |
Las estrategias como repetición y el uso de funciones comunicativas facilitan el aprendizaje en diversas áreas. |
|
|
|
x |
|
|
|
11 |
Infante, M., Isea, J., y Méndez, C. (2025). SciELO. |
Desarrollo del pensamiento crítico a partir de la praxis dialógica en el aula universitaria |
El diálogo conduce a un razonamiento lógico y a la reflexión, lo cual es esencial en el aprendizaje de la matemática. |
|
|
x |
|
|
|
|
12 |
Birgin, O., y Kübra, Y. (2021). Scopus/Web of Science. |
El efecto de la enseñanza de las matemáticas con el apoyo del software GeoGebra en la comprensión conceptual y la retención de los alumnos de octavo grado. |
El uso de herramientas tecnológicas en entornos online o mixtos facilitan la autogestión del aprendizaje. |
|
|
|
x |
|
|
|
13 |
Munaji, M., Rohaeti, T., Mutadi, M., Sumliyah, S., y Kodirun, K. (2025). Scopus/Web of Science. |
Revisión bibliográfica sobre la flexibilidad en las aulas de matemáticas interactivas: el papel de los profesores y los alumnos. |
La creatividad y flexibilidad constituyen aspectos clave en la enseñanza de la matemática. |
|
|
|
|
x |
|
|
14 |
De Vera, M., y Balgua, B. (2023). Scopus/Web of Science. |
Uso de tecnologías en la enseñanza de las matemáticas en un entorno de aprendizaje flexible. |
El uso de recursos digitales en la enseñanza de la matemática presenta desafíos, por cuanto es limitada en algunas zonas de Pangasinan, Filipinas, lo cual sucede también en otros países. |
|
|
|
|
x |
|
|
15 |
Oktaviani, W., Herman, T., y Darhim, D. (2022). Scopus/Web of Science. |
Diseño didáctico para mejorar la capacidad de razonamiento matemático de los estudiantes de secundaria sobre materiales de aplicación de derivadas. |
Un diseño didáctico para el aprendizaje de la matemática podría disminuir las dificultades de los estudiantes. |
|
|
|
|
x |
|
Elaboración: Los autores
Tal como se presenta en la tabla 1, se aplicaron criterios de pertinencia, evaluados mediante una escala de Likert con las siguientes categorías: 1= Sin pertinencia, 2 = Poco pertinente, 3 = Moderadamente pertinente, 4 = Pertinente y 5 = Muy pertinente. El análisis reveló los siguientes resultados: moderadamente pertinente (n=3), pertinente (n=5) y muy pertinente (n=7). Esto evidencia que los estudios considerados en la revisión sistemática demostraron una relevancia significativa.
DISCUSIÓN
Los resultados de la investigación indicaron que las diversas estrategias didácticas enfocadas en mejorar los procesos inferenciales en la resolución de problemas matemáticos a nivel de secundaria fueron relevantes. Dichos resultados resaltaron la efectividad de diversos enfoques que combinan metodologías activas, herramientas tecnológicas y recursos didácticos específicos (Litardo, 2023; Boice et al., 2024).
La comprensión lectora aunada a los procesos inferenciales constituyó un factor determinante, lo cual se evidencia en estudios como el de Rice y Wijekumar (2024), quienes señalan que los estudiantes con destrezas avanzadas en su comprensión lectora son más hábiles para resolver problemas numéricos que requieren de lógica, lo cual confirma que sí es posible unir diversas disciplinas enfocadas en el desarrollo de la comprensión lectora y el aprendizaje de la matemática.
Dentro del ámbito de la educación secundaria, se deben aprovechar diversas estrategias tanto individuales como grupales para la resolución de diversas tareas. Sin embargo, cuando se habla del aprendizaje de la matemática, es menester preparar y aplicar estrategias variadas entre las cuales se integre el trabajo cooperativo y la unificación con otras disciplinas, a fin de facilitar la resolución de problemas en situaciones determinadas (Isea y Méndez, 2025; Oktaviani et al., 2022). La idea es emplear una serie de situaciones hipotéticas que ayuden a los estudiantes a usar su lógica y prepararse para las vivencias que le ocurran en la vida diaria. Desde este punto de vista, de acuerdo con Dioses et al. (2024), manifiestan que las destrezas matemáticas se desarrollan al momento de activarse el pensamiento lógico e inferencial superando todo desafío latente. Por otra parte, la resolución de diversos problemas facilita el desarrollo del pensamiento inferencial, generando un compromiso mayor. Birgin y Kübra (2021), resaltan que el empleo de un software matemático aparte de ambientes virtuales de aprendizaje hace posible el desarrollo de la independencia estudiantil al momento de solucionar problemas numéricos. No obstante, cuando no se cuentan con estos recursos, el rendimiento se ve en descenso, limitando sus habilidades lógicas.
Desde otra visión, en concordancia con Oktaviani et al. (2022), es importante considerar que cuando se trabaja con estrategias bien diseñadas, los razonamientos numéricos se fortalecen, dando lugar a la comprensión y aplicación de problemas complejos. En este orden de ideas, cabe acotar que la integración de diversas tecnologías ha emergido como una vía apropiada para potenciar el aprendizaje mediante un desempeño positivo (Engelbrecht y Borba, 2024).
Por otro lado, es propicio destacar los beneficios del uso de los videos educativos, siendo Birgin y Kübra (2021), quienes argumentan esta afirmación. Según su aporte, estos autores afirman que los videos conducen a la comprensión de problemas complejos y a la autonomía estudiantil. De igual modo, Engelbrecht y Borba (2024), complementan el señalamiento de los anteriores autores, asegurando que el uso de las TIC, como el software y las plataformas interactivas, mejoran la comprensión de la matemática y, por ende, activan el razonamiento lógico.
Asimismo, vale decir que el diseño de diferentes recursos didácticos para el abordaje de la matemática ayuda a transformar la experiencia de aprendizaje en una forma más interactiva e inferencial. Por tanto, el empleo de materiales innovadores cónsonos con las demandas estudiantiles promueve una mayor asimilación y aplicación de saberes matemáticos. Es propicio señalar que la inclusión del pensamiento computacional en los planes de estudio optimiza la resolución de los problemas matemáticos por medio de componentes transversales asociados a la tecnología.
Para Orihuela (2025), el aprendizaje colaborativo constituye una estrategia clave para la solución de diversos problemas matemáticos, contribuyendo además a mejorar las relaciones interpersonales y el intercambio de saberes dentro de un entorno netamente educativo.
Como otro aspecto resaltante, se pudo precisar que las actividades individuales, grupales, así como la estructura administrativa-académica, también tienen mucho que ver con el logro del aprendizaje de los estudiantes; por este motivo, todos deben cooperar con un proceso de enseñanza activo y efectivo que prepare a los estudiantes para enfrentar situaciones de su vida diaria.
En otro orden de ideas, no se debe dejar de lado, la detección de diversos retos dentro del aprendizaje de la matemática, específicamente, en lo concerniente a la interpretación de enunciados numéricos complejos y en la toma de decisiones, lo cual conduce a la consideración de un andamiaje docente y a la implementación de tareas que activen el razonamiento lógico.
En resumen, los procesos inferenciales constituyen desafíos que requieren de la habilidad cognitiva para su abordaje. En tal sentido, la implementación de diversas estrategias didácticas novedosas e integradoras, contribuyen a la aplicación de metodologías activas que fortalecen la comprensión lectora y, por ende, el análisis de los problemas matemáticos.
Por último, este trabajo brinda un fundamento óptimo para futuros estudios enfocados en la enseñanza de la matemática. Los resultados obtenidos sugieren el uso del ABP (Aprendizaje basado en problemas) y del aprendizaje cooperativo han sido factores vitales para el desarrollo de las habilidades inferenciales. Uno de los autores que confirma esta apreciación es Orihuela (2025), quien encontró que las actividades cooperativas optimizan el rendimiento estudiantil en el área de matemática.
CONCLUSIONES
El empleo de metodologías interactivas como el ABP, el trabajo cooperativo y el uso de las TIC, han resultado ser efectivas para el desarrollo de las competencias inferenciales y matemáticas. Por tal razón, los docentes deben llevar a cabo estrategias centradas en el análisis crítico, ayudando a lograr un andamiaje apropiado para la interpretación y resolución de diversos problemas.
En este marco, se requiere de un enfoque interdisciplinario que integre las estrategias didácticas con las tecnológicas, a fin de llevar a cabo un proceso educativo innovador. Por lo antes planteado, los docentes deben permanecer con una actitud positiva frente a las transformaciones sociales y ajustar sus técnicas en función del fortalecimiento de su proceso de enseñanza en el área de la matemática. Asimismo, debe desarrollar procesos inferenciales que contribuyan al mejoramiento de las habilidades lógicas de sus aprendices.
Por último, el presente trabajo ha permitido analizar diversas vivencias relacionadas con el pensamiento inferencial y las habilidades matemáticas, aspectos que son fundamentales en el proceso educativo de los estudiantes; por ello, el mismo, ha abarcado temas relevantes que podrían beneficiar el desempeño académico de los aprendices y marcar un antes y un después para futuras investigaciones relacionadas con este tema.
FINANCIAMIENTO
No monetario.
AGRADECIMIENTOS
Gracias a quienes de forma meritoria cooperaron con el desarrollo del presente estudio.
REFERENCIAS CONSULTADAS
Bhor, A., y Varghese, M. (2024). Steam-based teaching: Enhancing quality in education. Journal of Education, 11(2), 323-331. https://n9.cl/c8hrd
Birgin, O., y Kübra, Y. (2021). The effect of GeoGebra software–supported mathematics instruction on eighth-grade students' conceptual understanding and retention. Journal of Computer Assisted Learning, 37(4), 925-939. https://n9.cl/l9un6
Boice, K., Alemdar, M., Jackson, J., Kessler, T., Choi, J., Grossman, S., y Usselman, M. (2024). Exploring teachers' understanding and implementation of STEAM: one size does not fit all. Frontiers in Education 9, 1-18. https://n9.cl/t53no
De Vera, M., y Balgua, B. (2023). Uso de tecnologías en la enseñanza de las matemáticas en un entorno de aprendizaje flexible. In International Conference on Information Technology and Mechatronics Engineering (Icitme), 2602(1), 030004. https://n9.cl/9z3wj
Dioses, L., Dios, M., y Sabino, C. (2024). Programa de estrategias de resolución de problemas para fortalecer el pensamiento divergente en matemática en estudiantes de secundaria. Universidad, Ciencia y Tecnología, 28(especial), 67-76. https://n9.cl/e22ubm
Engelbrecht, J., y Borba, M. C. (2024). Recent developments in using digital technology in mathematics education. ZDM–Mathematics Education, 56(2), 281-292. https://n9.cl/ajlef9
Gamarra, J., Duran, K., y Mucha, L. (2025). Impacto de las estrategias motivacionales en la resolución de problemas matemáticos en primaria. EPISTEME KOINONIA, 8(1), 402–423. https://n9.cl/r9oji
Gorbalan, I., Duran, K., y Mucha, L. (2025). Método Singapur para mejorar la resolución de problemas matemáticos en estudiantes de educación básica regular. EPISTEME KOINONIA, 8(1), 98–119. https://n9.cl/08ar9
Infante, M., Isea, J., y Méndez, C. (2025). Desarrollo del pensamiento crítico a partir de la praxis dialógica en el aula universitaria. Revista Conrado, 21(105), e 4697. https://n9.cl/ab0rj
Litardo, A. (2023). Las estrategias didácticas y el aprendizaje de las matemáticas en educación general básica. CIENCIAMATRIA, 9(2), 477-491. https://n9.cl/kyhhh
Molina, T., Lizcano, C., Burbano, L., y Isea, J. (2025). Discurso metacomunicativo como herramienta para el aprendizaje en el aula. Conrado, 21(103), 1-7. https://n9.cl/d5k2t
Munaji, M., Rohaeti, T., Mutadi, M., Sumliyah, S., y Kodirun, K. (2025). A literature review of flexibility in interactive mathematics classrooms: the role of teachers and students. Journal of Education and Learning (EduLearn), 19(2), 597-605. https://n9.cl/gn0dcn
Oktaviani, W., Herman, T., y Darhim, D. (2022). Didactic design to improve mathematical reasoning ability of high school students on derivative application materials. In AIP Conference Proceedings, 2577(1), 020047. https://n9.cl/uyunn
Orihuela, C. (2025). Estrategias de resolución de problemas matemáticos en estudiantes: una revisión sistemática. Revista InveCom, 5(1), 1-9. https://n9.cl/8qy83
Orihuela, C. (2025). Resolución de problemas y habilidades matemáticas en estudiantes de secundaria: Revisión sistemática. Revista Tribunal, 5(10), 573-584. https://n9.cl/fdo0k
Rice, M., y Wijekumar, K (2024). Inference skills for reading: A meta-analysis of instructional practices. Journal of educational psychology 116(4), 569–589. https://n9.cl/my7v2q
Soledispa, G., y Parra, S. (2024). Estrategias heurísticas en las capacidades de resolución de problemas matemáticos. Universidad, Ciencia y Tecnología, 28(especial), 88-97. https://n9.cl/z999h
Von Feigenblatt, O. F., Rivera, A., y Santiago, C. (2022). Scholarly publications in the 21st Century: The need for creativity and flexibility. "Ethics and Deontology" Journal, 2(01), 10-17. https://n9.cl/d8mwq
©2025 por los autores. Este artículo es de acceso abierto y distribuido según los términos y condiciones de la licencia CreativeCommons Atribución-NoComercial-CompartirIgual 4.0 Internacional (CC BY-NC-SA 4.0) (https://creativecommons.org/licenses/by-nc-sa/4.0/)