INTRODUCCIÓN
La educación tiene múltiples desafíos, uno de estos es formar personas competentes para un mundo moderno, por ende, una de las principales ramas es sin duda la matemática: ¿cómo se enseña?, ¿cómo se aprende? Entre otras interrogantes, son sin duda preguntas que se deben cotejar para así lograr buenos resultados.
En este sentido, el Instituto Nacional de Estadística e Informática (INEI, 2020) realizó un estudio donde se muestra que, en matemáticas, el 34.7% de los niños y el 33.3% de las niñas lograron resultados resaltantes en matemáticas, lo que en comparación al año 2018 muestra un aumento del 2.2% y 4.4% respectivamente. Pero, según enseñanza virtual para el aprendizaje (EVA), realizado por la Unidad de Medición de la Calidad (UMC, 2021) cuyos resultados en los estudiantes del 2° año de secundaria, nos muestran una caída de 13 puntos, en comparación con el año 2019, en el área de matemáticas, ubicando a nuestros alumnos en proceso.
En el nivel primario se observa que, hay un 50.2% correspondiente al ámbito rural que no han alcanzado los aprendizajes esperados para pasar del IV ciclo al V ciclo, mientras que en el ámbito urbano, esa cifra disminuye a un 29.8%. Lo que nos demuestra que el sector rural necesita más apoyo para lograr los aprendizajes esperados.
Así mismo, a nivel de la región La Libertad los estudiantes, según la UMC (2021), muestran un promedio regular en el área de matemáticas con respecto a otras regiones del país, destacando en los primeros lugares a regiones del sur como Tacna y a la regio Lima. Igualmente, a nivel local, según el INEI (2020), muestra que La Libertad en el 2019, en matemáticas, el 30.8% ha logrado el nivel satisfactorio, en comparación con el año 2018 donde solo alcanzaron el 25.7% de satisfacción en el área mencionada. Pero estas cifras, para el año 2021 según el UMC (2021), nos muestra que el 32.2% logró los aprendizajes esperados en matemáticas, es decir, estos alumnos son hábiles al solucionar problemas con números naturales que utilizan los gráficos estadísticos, el uso de tácticas en cálculos aritméticos, seriaciones, áreas y perímetros de figuras geométricas; y de valorar las nociones básicas en esta área. Es decir, solo un tercio de los alumnos beneficiados con las tabletas lograron los aprendizajes esperados en matemáticas.
Por ello, las estrategias de enseñanza son imprescindibles para el docente y requieren de eficacia, para lograr el desarrollo de las potencialidades de los estudiantes (Berrocal Ordaya y Palomino Rivera, 2022). En tal sentido, el proceso de enseñanza aprendizaje de la Matemática ha incorporado metodológicamente la resolución de problemas como un elemento central en su desarrollo (Vargas Rojas, 2021). Es así como, la resolución de problemas es una de las principales preocupaciones en el área de las matemáticas y suele suponer un reto para muchos estudiantes (Yupanqui Valverde, 2023).
En tal sentido, a nivel internacional tenemos a Díaz Gutiérrez (2024) con una investigación cualitativa, empleando un diseño fenomenológico, con una población de 210 alumnos. Se concluye que los maestros tienden a emplear métodos que vayan relacionados con su formación, por ende, sobresale lo tradicional por lo cual la evaluación es tomada como final y no como proceso.
Igualmente, a López Rengifo y Siuce Huatuco (2024) con una investigación cuantitativa, con diseño cuasiexperimental, con una población de 60 alumnos. La conclusión primordial es que existe diferencia significativa en los promedios de los estudiantes del que se intervino y que utilizaron el Álbum-Mátic, en la estrategia de Pólya, con un nivel de significancia de 0.05.
En este orden de ideas, la implementación del método Pólya, desde la etapa preoperacional del pensamiento matemático, reconoce la lectura en sus diferentes niveles como fundamento en la apropiación de habilidades a la hora de resolver problemas (Galvis Rivera y González Bautista, 2024). Además, según Tigse Parreño (2019) indica que para solucionar conflictos matemáticos, se inicia por reconocer los problemas con lo cual se generan múltiples respuestas. En otras palabras, los docentes son los llamados a generar en los discentes diversas estratagemas con la finalidad de promover aprendizajes duraderos, activos y relacionados con sus pares para así interesar a los alumnos por investigar. Esto conlleva a tomar en cuenta las ideas propias de cada persona, y la forma como aprenden el conocimiento, para que así los maestros puedan propiciar un análisis concienzudo de cómo aprenden y de la forma activa con que se adquieren los conocimientos.
Meneses y Peñaloza (2019) consideran que el método Pólya consiste en una serie de etapas, comenzando con la comprensión del problema, lo que implica analizar el enunciado para identificar con precisión lo que se solicita. En esta primera fase, se plantean interrogantes que facilitan el entendimiento, enfocándose en descubrir la incógnita, los datos disponibles y la suficiencia de la información proporcionada, entre otros aspectos, con el objetivo de lograr una mejor comprensión del problema.
El siguiente paso es la elaboración de un plan, una etapa caracterizada por la imaginación y la formulación de estrategias para resolver el problema identificado. En este proceso, se plantean preguntas orientadas a ayudar al estudiante a elegir la estrategia más adecuada, considerando problemas similares, métodos de solución previos y la reformulación del enunciado y la respuesta esperada. Es fundamental brindar el apoyo necesario para que los estudiantes utilicen la estrategia más pertinente.
Con base en estos planteamientos, el objetivo general de la investigación es analizar las estrategias del método Pólya para fomentar la creación de problemas matemáticos en estudiantes de educación básica regular
MÉTODO
Según Hernández et al. (2014) el enfoque de esta investigación es cuantitativo y es característico de este enfoque realizar mediciones utilizando la objetividad y la generalización de los resultados. La población está conformada por 25 alumnos que están divididos en 15 niños y 10 niñas siendo todos los estudiantes del V ciclo de Educación Primaria del distrito de Lucma, de Gran Chimú 2024. Se emplea el muestreo probabilístico intencional puesto que todos los estudiantes de dicho ciclo de estudio serán seleccionados para este experimento. Así las unidades de análisis lo constituyen los estudiantes del V ciclo de una institución educativa de Lucma del nivel Primaria. Como instrumento se utiliza una prueba objetiva en el pre test y post test. Se plantea además el método analítico-sintético por medio del cual, se descompone un todo en partes extrayendo cualidades, componentes, relaciones y más para posteriormente unir las partes analizadas y con ello descubrir características y relaciones entre los elementos (Rodríguez y Pérez, 2017).
RESULTADOS
Se presentan a continuación los resultados obtenidos.
Tabla 1.
Estadísticos Descriptivos Del Pre y Post Test de la Estrategia Pólya.
|
ESTADISTICOS |
PRE-TEST |
POST TEST |
|
N Válido |
25 |
25 |
|
Perdidos |
0 |
0 |
|
Media |
9.48 |
18.88 |
|
Error estándar de la media |
.883 |
.194 |
|
Mediana |
8.00 |
19.00 |
|
Moda |
6 |
19a |
|
Desv. Desviación |
4.417 |
.971 |
|
Varianza |
19.510 |
.943 |
|
Asimetría |
.934 |
-.336 |
|
Error estándar de asimetría |
.464 |
.464 |
|
Coeficiente de Variación |
46 |
5.1 |
|
Error estándar de curtosis |
.902 |
.902 |
|
Rango |
15 |
3 |
|
Mínimo |
5 |
17 |
|
Máximo |
20 |
20 |
Elaboración: Los autores.
Los resultados evidencian diferencias significativas en la creación de problemas matemáticos (Tabla 1). Durante las primeras pruebas, las medidas de tendencia central resultaron 9.48; 8 y 6, con una desviación estándar de 4.417. No obstante, en las pruebas finales, las tendencias centrales se situaron en 18.88; 19 y 19, con una desviación estándar inferior a 0.971, lo que evidencia un desempeño más uniforme. La distribución de los resultados en las pruebas finales presenta una asimetría negativa, lo que sugiere que la mayoría de los estudiantes obtuvieron calificaciones altas, pero algunos pocos tuvieron calificaciones significativamente más bajas. En comparación, las pruebas iniciales mostraron una distribución casi simétrica. Adicionalmente, el coeficiente de variación aportó datos adicionales acerca de la coherencia de los resultados. Durante las pruebas preliminares, se registró una heterogeneidad del 46% en el nivel de conocimiento de creación de problemas matemáticos, en las pruebas finales, el coeficiente bajó al 5.1%, lo que indica que las notas fueron más homogéneas en la muestra de estudio.
Tabla 2.
Estadísticos comparativos de la creación de problemas matemáticos en sus dimensiones.
|
Estadisticos |
Requerimiento |
Contexto |
Entorno |
Matemático |
||||
|
|
Pre |
Post |
Pre |
Post |
Pre |
Post |
Pre |
Post |
|
N Válido |
25 |
25 |
25 |
25 |
25 |
25 |
25 |
25 |
|
Perdidos |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
Media |
2.72 |
4.56 |
2.28 |
4.88 |
2.52 |
4.72 |
1.88 |
4.64 |
|
Error estándar de la media |
.242 |
.117 |
.262 |
.066 |
.295 |
.092 |
.260 |
.098 |
|
Mediana |
3.00 |
5.00 |
2.00 |
5.00 |
2.00 |
5.00 |
2.00 |
5.00 |
|
Moda |
2 |
5 |
2 |
5 |
1 |
5 |
1 |
5 |
|
Desv. Desviación |
1.208 |
.583 |
1.308 |
.332 |
1.475 |
.458 |
1.301 |
.490 |
|
Varianza |
1.460 |
.340 |
1.710 |
.110 |
2.177 |
.210 |
1.693 |
.240 |
|
Asimetría |
.282 |
-.936 |
.405 |
-2.491 |
.508 |
-1.044 |
.610 |
-.621 |
|
Error estándar de asimetría |
.464 |
.464 |
.464 |
.464 |
.464 |
.464 |
.464 |
.464 |
|
Coeficiente de Variación |
44 |
12 |
57 |
6 |
58 |
9 |
69 |
10 |
|
Error estándar de curtosis |
.902 |
.902 |
.902 |
.902 |
.902 |
.902 |
.902 |
.902 |
|
Rango |
4 |
2 |
5 |
1 |
4 |
1 |
5 |
1 |
|
Mínimo |
1 |
3 |
0 |
4 |
1 |
4 |
0 |
4 |
|
Máximo |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
Elaboración: Los autores.
Los resultados revelan diferencias significativas entre las distintas dimensiones en la creación de problemas matemáticos. En las pruebas iniciales, las medidas de tendencia central para las dimensiones fueron las siguientes: en información (2.72; 3 y 2), requerimiento (2.28; 2 y 2), contexto (2.52; 2 y 1), y entorno matemático (1.88; 2 y 1), con desviaciones estándar de 1.208; 1.308; 1.475 y 1.301 respectivamente. En lo referido a las evaluaciones finales, las tendencias centrales mejoraron significativamente en todas las dimensiones: información (4.56; 5 y 5), requerimiento (4.88; 5 y 5), contexto (4.72; 5 y 5) y entorno matemático (4.64; 5 y 5), con desviaciones estándar de 0.583; 0.332; 0.458 y 0.490. Además, se observa que la distribución en las pruebas finales presenta asimetría negativa, mientras que en las pruebas iniciales las distribuciones eran casi simétricas. Adicionalmente, el coeficiente de variación muestra una heterogeneidad en las pruebas iniciales de 44%, 57%, 58% y 69% para las diferentes dimensiones. En las pruebas finales, este coeficiente aumentó ligeramente a 12%, 6%, 9% y 10%, lo que indica una homogeneidad en las muestras de estudios.
En definitiva, en las dimensiones de la creación de problemas matemáticos, el promedio se incrementó de 9,48 a 18,88, mientras que la desviación estándar disminuyo de 4,417 a 0,971 y el coeficiente de variación se redujo de 46% a 5,1%. Es así que, en la educación primaria se trabaja la resolución de problemas mas no la creación puesto que esto representa una estrategia más completa para mejorar las habilidades en el área de matemáticas. En ese sentido, los resultados obtenidos en la creación de problemas matemáticos evidencian un claro aumento en los promedios de los estudiantes, lo que repercutirá en mejoras al momento de resolverlos, pues no solo se ceñirán a ejecutar una estrategia de solución, sino que crearán una nueva forma de producir problemas relacionándolos con su entono.
Para finalizar, según Meneses y Peñaloza (2019) la estrategia Pólya se compone de una serie de etapas, comenzando con la comprensión del problema, lo que implica analizar el enunciado para identificar con precisión lo que se solicita. En esta primera fase, se plantean interrogantes que facilitan el entendimiento, enfocándose en descubrir la incógnita, los datos disponibles y la suficiencia de la información proporcionada, entre otros aspectos, con el objetivo de lograr una mejor comprensión del problema.
El siguiente paso es la elaboración de un plan, una etapa en la que, a través de la imaginación, se generan estrategias para resolver el problema identificado. En este proceso, se plantean preguntas orientadas a guiar al estudiante en la búsqueda de la mejor estrategia, considerando problemas similares, métodos de solución previos y la reformulación tanto del enunciado como de la respuesta esperada. Es fundamental brindar el apoyo necesario para que los estudiantes utilicen la estrategia más pertinente.
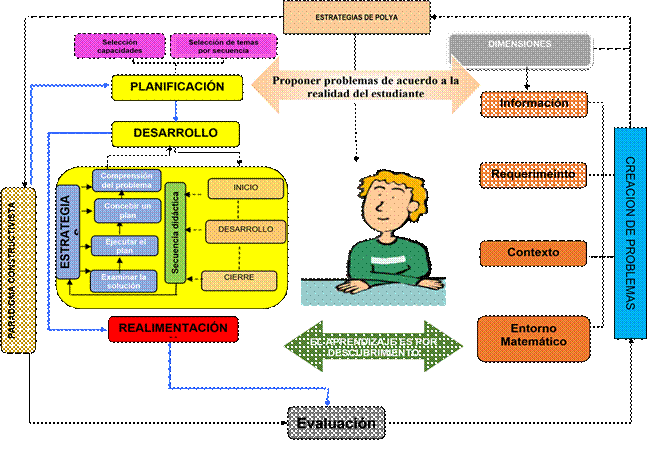
(Figura 1).
Figura 1. Estrategias.
Elaboración: Los autores.
CONCLUSIONES
Es necesario incentivar a los docentes con el tema de creación de problemas pues trabaja de forma completa el área de matemáticas, ya que no solo se circunscribe a solucionar un problema, sino que desafía a los alumnos a crear situaciones parecidas a los problemas dados y con ello se apropia con mayor significatividad el tema a aprender.
FINANCIAMIENTO
No monetario.
AGRADECIMIENTO
A la universidad César Vallejo, por el apoyo institucional.
REFERENCIAS CONSULTADAS
Berrocal Ordaya, C., y Palomino Rivera, A. (2022). Capacidad de resolución de problemas matemáticos y su relación con las estrategias de enseñanza en estudiantes del primer grado de secundaria. Educación matemática, 34(2), 275-288. https://doi.org/10.24844/em3402.10
Díaz Gutiérrez, E. (2024). Assessment Practices in Costa Rican Mathematics Teachers. Revista Digital: Matemática, Educación E Internet, 24(2). https://doi.org/10.18845/rdmei.v24i2.6902
Galvis Rivera, Y., & González Bautista, E. (2024). Incidencia del Enfoque Resolución de Problemas de George Pólya en el Desarrollo del Pensamiento Variacional. Revista Tecnológica-Educativa Docentes 2.0, 17(1), 149-160. https://doi.org/10.37843/rted.v17i1.447
Hernández, R., Fernández, C., y Baptista, M. (2014). Metodología de la Investigación. (6ta. ed.). McGraw-Hill. https://n9.cl/t6g8vh
INEI. (2020). Perú. Indicadores de Educación por departamentos, 2009–2019. https://n9.cl/jlqu6
López Rengifo, C. F., y Siuce Huatuco, D. J. (2024). El Álbum-Mátic en la estrategia de Pólya para desarrollar competencias matemáticas. Cuadernos de Investigación Educativa, 15(2). https://doi.org/10.18861/cied.2024.15.2.3718
Meneses, M., y Peñaloza, D. (2019). Método de Pólya como estrategia pedagógica para fortalecer la competencia resolución de problemas matemáticos con operaciones básicas. Zona Próxima, 31, 7-25. https://n9.cl/6fw3a
Rodríguez, A., y Pérez, A. O. (2017). Métodos científicos de indagación y de construcción del conocimiento. Revista EAN, 82, 179-200. https://doi.org/10.21158/01208160.n82.2017.1647
Tigse Parreño, C. M. (2019). El Constructivismo, según bases teóricas de César Coll. Revista Andina De Educación, 2(1), 25-28. https://doi.org/10.32719/26312816.2019.2.1.4
UMC. (2021). Entorno Virtual de Aprendizaje EVA. https://n9.cl/pc4lmd
Vargas Rojas, W. (2021). La resolución de problemas y el desarrollo del pensamiento matemático. Horizontes Revista de Investigación en Ciencias de la Educación, 5(17), 230-251. https://doi.org/10.33996/revistahorizontes.v5i17.169
Yupanqui Valverde, Y. N. (2023). Estrategias didácticas para la resolución de problemas matemáticos en alumnos de educación básica regular. Horizontes. Revista De Investigación En Ciencias De La Educación, 7(30), 1903. https://doi.org/10.33996/revistahorizontes.v7i30.638