RESUMEN
El propósito del estudio fue determinar la efectividad de la aplicación del método Singapur en la resolución de problemas matemáticos en estudiantes de segundo grado de una institución educativa de Trujillo. La investigación fue de tipo aplicada con diseño cuasiexperimental. La población estuvo conformada por 132 estudiantes con un grupo control y experimental de 21 estudiantes. El muestreo fue no probabilístico por conveniencia. La técnica de recolección de datos fue a través de una prueba objetiva de resolución de problemas aritméticos de enunciado verbal constituida por 10 ítems distribuidos en 4 dimensiones: combinación, cambio, comparación e igualación. Los resultados fueron analizados mediante la prueba de normalidad de Shapiro- Wilk y la prueba de hipótesis T- student. Se aceptó la hipótesis general al concluir que el método aplicado mejoró significativamente la resolución de problemas matemáticos en estudiantes de segundo grado.
Descriptores: Método; problemas matemáticos; enunciado verbal. (Tesauro UNESCO).
ABSTRACT
The purpose of the study was to determine the effectiveness of the application of the Singapore method in solving mathematical problems in second grade students of an educational institution in Trujillo. The research was applied with a quasi-experimental design. The population consisted of 132 students with a control and experimental group of 21 students. The sampling was non-probabilistic by convenience. The data collection technique was through an objective test of arithmetic problem solving with verbal statements consisting of 10 items distributed in 4 dimensions: combination, change, comparison and equalization. The results were analyzed using the Shapiro-Wilk normality test and the student’s t-hypothesis test. The general hypothesis was accepted when concluding that the applied method significantly improved mathematical problem solving in second grade students.
Descriptors: Method; mathematical problems; word statement. (UNESCO Thesaurus).
INTRODUCCIÓN
En el contexto educativo actual, la adquisición de competencias matemáticas sólidas se ha convertido en un elemento fundamental para el desarrollo integral de los estudiantes (Acosta, 2024; Llamazares y Arias, 2022). “La competencia adquiere así una connotación más amplia, significa que la información adquirida a través de la alfabetización puede ayudar a la construcción ciudadana y democrática, y a la comprensión del mundo en que se vive” (Tramallino y Zeni, 2024, p. 41). Por esta razón, se busca evaluar la efectividad de una estrategia innovadora denominada Método Singapur, cuyo objetivo es mejorar la capacidad de resolución de problemas matemáticos en estudiantes de los primeros grados de educación básica.
La importancia de esta estrategia radica en su potencial para optimizar la enseñanza de las matemáticas, ofreciendo a los educadores una herramienta pedagógica efectiva que fomente el desarrollo del pensamiento lógico y la comprensión profunda de los conceptos matemáticos (Cuasapud y Quintana. 2023). Esta iniciativa surge como respuesta a los desafíos observados en el ámbito educativo, donde se identifica una creciente necesidad de fortalecer las habilidades matemáticas desde una edad temprana mediante estrategias motivadoras, ya que estas competencias son esenciales para el éxito académico y el desempeño en la sociedad contemporánea (Rodríguez y Duran, 2023).
A lo largo de los últimos años, la Organización de las Naciones Unidas para la Educación, la Ciencia y la Cultura (UNESCO, 2015) ha recopilado información significativa sobre el rendimiento académico de estudiantes que están cursando o a punto de finalizar su educación básica, mediante evaluaciones internacionales. El promedio de puntuación en la OCDE disminuyó 15 puntos en comparación con 2018, alcanzando un total de 472 puntos.
A consecuencia de la crisis sanitaria, se preveía un incremento en la proporción de estudiantes de educación básica que no lograrían los estándares mínimos en habilidades matemáticas. Esta situación se debió a varios factores, como el cierre prolongado de las escuelas, la brecha digital y las dificultades económicas que enfrentaron muchas familias (Medina, 2021). Además, la pandemia exacerbó las desigualdades educativas preexistentes y los estudiantes de países de bajos ingresos y de hogares desfavorecidos fueron los más afectados. Estos estudiantes tuvieron menos posibilidades de tener una educación de calidad y de emplear recursos que les permitieran desarrollar habilidades matemáticas sólidas durante la pandemia.
En consecuencia, se preveía una expansión adicional de la disparidad en el dominio matemático, lo cual potencialmente impactaría a largo plazo tanto en la formación del talento humano como en las perspectivas económicas de los estudiantes perjudicados.
Esta realidad condujo a los países a formarse en el área de la tecnología hasta mostrar avances en el empleo de estrategias digitales efectivas (Lever, 2020; Medina, 2021). Esto surgió por razones como la carencia de herramientas digitales y materiales didácticos, la limitada capacidad de los tutores para respaldar el estudio doméstico y la mayor tendencia de los estudiantes de entornos menos privilegiados a desertar del sistema educativo por apuros financieros (Garzón et al., 2022; Lugo et al., 2019).
De acuerdo con Cuasapud y Quintana (2023), el uso del método Singapur en la enseñanza matemática ha sido exitoso. El método se fundamenta en dos principios clave: el enfoque Concreto, Pictórico y Abstracto, así como la idea de dominio. Este enfoque introduce conceptos matemáticos abstractos de manera tangible, avanzando gradualmente hacia ideas más complejas. Esta metodología presenta nociones matemáticas abstractas de forma accesible, facilitando la transición hacia conceptos más sofisticados. Esto permite a los estudiantes asimilar mejor los conceptos matemáticos al relacionarlos con elementos y situaciones del mundo real antes de pasar a representaciones más teóricas.
En nuestro país, a partir de la evaluación realizada en el 2022 por Pisa, el Perú ocupa el puesto 59, lo cual manifiesta que el Perú subió unos cuantos peldaños en comparación con los resultados del 2018, pero estadísticamente esta diferencia no es significativa. Por lo antes dicho, en nuestro país se ha mostrado interés por el método Singapur y, por ende, se han realizado algunos esfuerzos para implementarlo, aunque no de manera generalizada. En el sistema educativo nacional, se ha incorporado indirectamente dentro de sus procesos pedagógicos, al seguir procesos concretos y pictóricos que recaen en la utilización de representaciones simbólicas. A nivel local y dadas las circunstancias por la pandemia del COVID, los estudiantes de la región no han logrado desarrollar las competencias para su grado. Frente a esta situación, es crucial llevar a cabo acciones inmediatas para enfrentar los desafíos relacionados con la resolución de problemas. Dentro de este tenor, “el conflicto cognitivo ya es considerado como un elemento importante del currículo y de las actividades docentes como alguna actividad pedagógica en la sesión de aprendizaje”. (Manrique et al., 2021, p. 20). Por tanto, los docentes deben desempeñar un papel central en la adopción de estrategias innovadoras y efectivas que guíen sus procesos pedagógicos (Majul et al., 2021; García, 2019).
Por consiguiente, se sugiere que “los profesores deben centrarse en la resolución de problemas y desarrollar estrategias que alienten a los estudiantes a pensar críticamente” (Orihuela, 2025, p. 1). Villarreal et al. (2019) expresan que “se debe promover en los docentes mayor compromiso con la renovación del conocimiento y la información, así como estimular la creación de contenido digital que fomente las competencias en el alumnado” (p. 3). Por ende, es esencial capacitar a los maestros en el Método Singapur, dotándolos de las herramientas y recursos necesarios para su adecuada implementación en el aula. Además, los directivos deben asegurar un seguimiento constante, proporcionando asesoramiento y retroalimentación a los docentes para maximizar la efectividad de este enfoque.
Cabe destacar que al buscar fortalecer las competencias matemáticas desde una etapa temprana, esta iniciativa investigativa contribuye a consolidar bases sólidas para el rendimiento académico futuro de los estudiantes. Asimismo, al propiciar el desarrollo del pensamiento lógico y la resolución de problemas, se cultivan competencias fundamentales para la vida, preparando a los educandos para afrontar desafíos en diversos contextos.
El escenario de investigación se sitúa en una institución educativa pública de Trujillo, donde una evaluación diagnóstica en matemáticas realizada durante marzo reveló datos preocupantes en la competencia de resolución de problemas, donde solo un 26% de estudiantes de segundo grado alcanzó los aprendizajes esperados, mientras que un 42% está en proceso y un 32% en nivel inicio. Este diagnóstico evidencia deficiencias significativas en la comprensión y aplicación de conceptos matemáticos fundamentales, lo cual podría impactar adversamente en el desarrollo académico posterior de los estudiantes.
Las causas detrás de este bajo rendimiento están vinculadas a la falta de estrategias pedagógicas efectivas que fomenten el pensamiento lógico-matemático y la resolución de problemas. En este marco, el Método Singapur emerge como una solución metodológica innovadora para subsanar estas dificultades. Esta metodología destaca por su énfasis en la comprensión conceptual y el empleo de representaciones pictóricas, proporcionando a los estudiantes una herramienta eficaz para resolver problemas matemáticos. Sin embargo, la falta de familiaridad por parte de los docentes con este método y la necesidad de adaptar los materiales al contexto local constituyen desafíos significativos para su implementación.
En virtud de lo descrito, resulta necesario resolver la siguiente interrogante: ¿En qué medida el Método Singapur mejora la resolución de problemas matemáticos en estudiantes de segundo grado de una institución educativa de Trujillo? Desde esta incógnita, emergió como objetivo general: determinar la efectividad de la aplicación del método Singapur en la resolución de problemas matemáticos en estudiantes de segundo grado de una institución educativa de Trujillo.
Más allá de simplemente encontrar una solución, esta actividad podría estimular en los estudiantes formas más elevadas de pensamiento, por cuanto cada problema matemático tiene características propias, por lo que las estrategias de resolución varían según el caso, sin poder generalizar un único método aplicable a todos los desafíos, sabiendo además, que “cada estudiante adquiere de diferentes formas el conocimiento”. (Solórzano et al., 2020, p. 160).
El enfoque de investigación fue cuantitativo, cuyo objetivo fue probar o validar una teoría ya establecida. El método utilizado fue hipotético-deductivo. La investigación se clasificó como aplicada. El diseño fue de tipo cuasi experimental para comparar grupos que se habían formado en función de condiciones específicas.
La población estuvo compuesta por estudiantes de segundo grado de primaria de una institución pública de Trujillo, que equivale a 132 niñas, con un promedio de aproximadamente 20 estudiantes por sección. La muestra fue de tipo no probabilística, por lo que no se utilizó una fórmula para su determinación, por tanto, el aula de segundo grado B se seleccionó al azar, conformado por 21 estudiantes, siendo este el grupo experimental, al cual se le aplicó la propuesta, mientras que el grupo control lo asumió el segundo grado C. Este tipo de muestreo exigió el cumplimiento de criterios específicos de inclusión y exclusión, así como características y condiciones particulares, para el logro de los objetivos. En lo que respecta al criterio de inclusión, se consideraron todos los alumnos de segundo grado inscritos en las listas correspondientes al año 2024 y que asistían con regularidad. No se estableció ningún criterio de exclusión.
Para esta investigación se utilizó como técnica el test mediante la Prueba de resolución de problemas aritméticos de enunciado verbal para 2° de primaria conformada por 10 ítems que evaluaron las 4 dimensiones de la variable. La prueba se aplicó en forma física a los estudiantes del grupo control y experimental.
Para determinar la validez del instrumento, se solicitó la evaluación de cinco especialistas en matemáticas y educación primaria. Tras realizar los ajustes necesarios, los especialistas emitieron una valoración positiva, indicando así una adecuada validez de contenido del instrumento. En cuanto a la confiabilidad del instrumento, se realizó una prueba piloto inicial con un grupo de estudiantes que tenían rasgos parecidos a los de la población objetivo del estudio. Posteriormente, se analizaron los datos obtenidos utilizando la técnica de división por mitades (Split-half), cuyos resultados mostraron que el instrumento presentó un alto nivel de confiabilidad.
Para el análisis de los datos recolectados, se utilizó el software estadístico IBM SPSS en su versión 26. Para la confiabilidad del instrumento, se determinó que fue de 0.898, lo que indicó un nivel aceptable de confiabilidad.
RESULTADOS
A continuación se muestran los resultados derivados de la Prueba de Resolución de problemas de enunciado verbal de los sujetos investigados. La misma constó de 10 ítems que miden la resolución de problemas matemáticos, en sus dimensiones. Se muestran los hallazgos en tablas con su respectiva interpretación y teniendo en cuenta el orden de los objetivos propuestos.
Resultados descriptivos
Según la tabla 1, después de implementar el programa de Método Singapur para mejorar la resolución problemas matemáticos y realizar la comparación de las medias, se obtuvo un puntaje de 8,35 en el pretest y de 16,07 en el postest. Se observa una clara diferencia entre las medidas de tendencia central, destacándose principalmente la media seguida por la mediana y la moda.
Tabla 1.
Estadísticos descriptivos del pre y post test de la prueba de resolución de problemas matemáticos a estudiantes de segundo grado de una institución educativa de Trujillo.
|
Descriptivos |
Prueba Inicial |
Prueba Final |
|
Media |
8,35 |
16,07 |
|
Error típico |
0,61 |
0,45 |
|
Mediana |
7,5 |
16 |
|
Moda |
7 |
18 |
|
Desviación estándar |
2,81 |
2,07 |
|
Varianza de la muestra |
7,90 |
4,30 |
|
Curtosis |
0,22 |
-0,61 |
|
Coeficiente de asimetría |
0,31 |
-0,62 |
|
Rango |
12 |
7 |
|
Mínimo |
3 |
12 |
|
Máximo |
15 |
19 |
|
Coeficiente de Variación |
0,34 |
0,13 |
|
Cuenta |
21 |
21 |
|
Nivel de confianza (95.0%) |
1,27 |
0,94 |
Elaboración: Los autores.
El coeficiente de desviación estándar disminuyó de 2,81 a 2,07 y la varianza se redujo de 7,90 a 4,30. Además, la variación del coeficiente pasó de 0,31 a – 0,62. Estos cambios indican que, tras la intervención, los resultados se volvieron más homogéneos, lo que sugiere que el método Singapur mejora la resolución de problemas matemáticos.
En el pretest, el puntaje mínimo fue de 3 y el máximo de 15 con un rango de 12. En el postest, el valor más bajo fue de 12 y el más alto de 19, con un rango de 7. Esta modificación muestra un avance notable en el desempeño, dado que incluso la puntuación más baja del postest (12) sobrepasa la puntuación media del pretest y se sitúa por encima del puntaje máximo obtenido en la evaluación inicial.
La asimetría disminuyó de 0,31 a -0,62, manteniendo un valor negativo que indica una inclinación hace la izquierda. Esta reducción supone que la intervención mediante el método singapur ayudó a reducir las disparidades significativas entre los estudiantes, mejorando su desempeño en la resolución de problemas matemáticos de aquellos estudiantes con calificaciones bajas y logrando una distribución de puntuaciones más equitativa. Ambos valores de asimetría (-0,31 y -0,62) se encuentran dentro del rango comúnmente aceptado. Se observó un cambio de una distribución ligeramente asimétrica positiva en el pretest (0,31) a una asimetría negativa en el postest (-0,62), lo que evidencia una curva con tendencia negativa en la evaluación final.
Tabla 2.
Estadísticos comparativos de la resolución de problemas matemáticos en sus dimensiones.
|
Dimensión |
Combinación |
Cambio |
Comparación |
Igualación |
||||
|
Descriptivos |
Pre |
Pos |
Pre |
Pos |
Pre |
Pos |
Pre |
Pos |
|
Media |
1,024 |
1,786 |
3,095 |
4,476 |
2,571 |
4,905 |
1,667 |
4,905 |
|
Error típico |
0,122 |
0,055 |
0,245 |
0,248 |
0,321 |
0,168 |
0,232 |
0,266 |
|
Mediana |
1 |
2 |
3 |
4,5 |
2 |
5 |
1 |
5 |
|
Moda |
1 |
2 |
3,5 |
3,5 |
2 |
5 |
1 |
6 |
|
Desviación estándar |
0,558 |
0,254 |
1,125 |
1,134 |
1,469 |
0,768 |
1,065 |
1,221 |
|
Varianza de la muestra |
0,312 |
0,064 |
1,265 |
1,287 |
2,157 |
0,590 |
1,133 |
1,490 |
|
Curtosis |
-0,335 |
-2,115 |
-0,697 |
-1,331 |
0,482 |
0,676 |
-0,377 |
-0,068 |
|
Coeficiente de asimetría |
-0,102 |
-0,311 |
0,058 |
-0,077 |
0,735 |
-0,561 |
0,478 |
-0,895 |
|
Rango |
2 |
0,5 |
4 |
3,5 |
6 |
3 |
4 |
4 |
|
Mínimo |
0 |
1,5 |
1 |
2,5 |
0 |
3 |
0 |
2 |
|
Máximo |
2 |
2 |
5 |
6 |
6 |
6 |
4 |
6 |
|
Coeficiente de variación |
0,54 |
0,14 |
0,36 |
0,25 |
0,57 |
0,16 |
0,64 |
0,25 |
|
Cuenta |
21 |
21 |
21 |
21 |
21 |
21 |
21 |
21 |
|
Nivel de confianza |
0,254 |
0,115 |
0,512 |
0,516 |
0,669 |
0,350 |
0,485 |
0,556 |
Elaboración: Los autores.
Según la tabla 2, los resultados revelan mejoras significativas en todas las dimensiones al comparar el grupo experimental con el grupo control. La dimensión Igualación mostró el avance más notable con una diferencia de 3,2 puntos (GC: 1.6; GE: 4,9) y la mayor consistencia en el grupo experimental (coeficiente de variación: 5%). La dimensión Combinación presentó el menor avance con 0,7 puntos de diferencia, mientras que Cambio y Comparación mostraron avances intermedios (1,3 y 1,9 puntos respectivamente). En todas las dimensiones, el grupo experimental alcanzó medias superiores a 16 puntos, con una dispersión notablemente menor (CV: 15-25%), evidenciando la efectividad de la intervención experimental.
Análisis ligado a la hipótesis Prueba de normalidad
En la tabla 3, se plantean las hipótesis estadísticas para el análisis, utilizando un nivel de significancia α=0.05
𝐻0: Si el p-valor (sig.) >0,05, los datos siguen una distribución normal.
𝐻𝑎: Si el p-valor (sig.) < 0,05, los datos no siguen una distribución normal.
Tabla 3.
Prueba de normalidad para el grupo control y experimental.
|
Shapiro Wilk |
||||
|
Grupo |
Variable / Dimensiones |
Estadístico |
gl |
Sig. |
|
Experimental |
Resolución de problemas matemáticos |
0,922 |
21 |
0,007 |
|
Combinación |
0,928 |
21 |
0,011 |
|
|
Cambio |
0,926 |
21 |
0,009 |
|
|
Comparación |
0,944 |
21 |
0,038 |
|
|
Igualación |
0,907 |
21 |
0,002 |
|
|
Control |
Resolución de problemas matemáticos |
0,913 |
21 |
0,004 |
|
Combinación |
0,931 |
21 |
0,014 |
|
|
Cambio |
0,918 |
21 |
0,005 |
|
|
Comparación |
0,916 |
21 |
0,004 |
|
|
Igualación |
0,891 |
21 |
0,001 |
|
Elaboración: Los autores.
De los valores obtenidos en la prueba de normalidad de Shapiro Wilk, la misma que se aplicó por tener una muestra menor a 50, de todos los valores tanto en el grupo experimental y control, se ha obtenido que la significancia en la variable principal y sus dimensiones son menores al 0,05, con lo cual se rechaza la hipótesis de normalidad.
Apreciaciones por considerar en la Contrastación de hipótesis específicas.
Hipótesis general
𝑯𝟎: µ𝑮𝑪𝒑𝒐𝒔 =µ𝑮𝑬𝑿𝒑𝒐𝒔 (No hay diferencias entre la post prueba del grupo experimental y grupo control)
𝑯𝟏: µ𝑮𝑪𝒑𝒐𝒔 =µ𝑮𝑬𝑿𝒑𝒐𝒔 (Si hay diferencias entre la post prueba del grupo experimental y grupo control)
Nivel de significancia
𝑝 ≥ 0.05: Aceptamos la hipótesis nula p <0.05∶ Rechazamos la hipótesis nula.
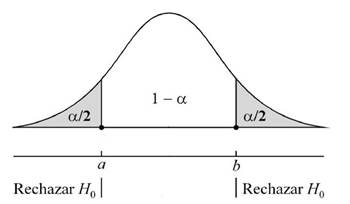
Figura 1. Regla de decisión.
Elaboración: Los autores.
De acuerdo con la figura 1, si el p-valor <0,05: se rechaza Ho, lo que implica que el Método Singapur ha tenido un impacto positivo y significativo en la resolución de problemas matemáticos. Si el p-valor >0,05: No se rechaza Ho, lo que sugiere que no hay evidencia suficiente para afirmar que el Método Singapur ha mejorado significativamente la resolución de problemas matemáticos.
Cálculo de la prueba de hipótesis para evaluar diferencia de medias del pre y postest del grupo control y experimental
De acuerdo con los estadísticos analizados, tomando en cuenta la regla de decisión, se concluye que existe diferencia significativa en la resolución de problemas matemáticos en estudiantes de segundo grado de una institución educativa de Trujillo, después de haber aplicado el Método Singapur, pues se tiene un valor de p<0,05, aceptándose la hipótesis alterna de desigualdad de medias. Al evaluar los promedios, podemos identificar que en el pretest se tiene una nota promedio de 8,36 y en el postest de 16,07, finalmente, se puede observar que los mejores resultados en el postest se presentaron en el grupo experimental; confirmando que el método aplicado mejora significativamente la resolución problemas matemáticos. Se puede decidir que, al ser p <0,05: aceptamos la hipótesis de investigación y rechazamos la hipótesis nula; por lo tanto, se puede señalar que existe diferencia significativa entre las medias del pre y postest aplicado entre el grupo experimental y el grupo control para la variable dependiente.
Cálculo de la prueba de hipótesis para evaluar diferencia de medias del pre y postest del grupo control y experimental para la dimensión combinación
De acuerdo con los estadísticos analizados y tomando en cuenta la regla de decisión, se concluye que existe diferencia significativa en la dimensión combinación de la resolución de problemas matemáticos en estudiantes de segundo grado de una institución educativa de Trujillo, después de haber aplicado el Método Singapur, pues se tiene un valor de p<0,05, aceptándose la hipótesis alterna de desigualdad de medias. Al evaluar los promedios, podemos identificar que en el pretest se tiene una nota promedio de 1,02 y en el postest de 1,79, finalmente, se puede observar que los mejores resultados en el postest se presentaron en el grupo experimental; confirmando que el método aplicado mejora significativamente en la dimensión combinación de la resolución de problemas matemáticos en estudiantes de segundo grado. Se puede decidir que, al ser p < 0,05: nos permite aceptar la hipótesis de investigación y rechazar la hipótesis nula.
Cálculo de la prueba de hipótesis para evaluar diferencia de medias del pre y postest del grupo control y experimental para la dimensión cambio.
De acuerdo con los estadísticos analizados y tomando en cuenta la regla de decisión, se concluye que existe diferencia significativa en la dimensión cambio de la resolución de problemas matemáticos en estudiantes de segundo grado de una institución educativa de Trujillo, después de haber aplicado el Método Singapur, pues se tiene un valor de p<0,05, aceptándose la hipótesis alterna de desigualdad de medias. Al evaluar los promedios, podemos identificar que en el pretest, se tiene una nota promedio de 3,09 y en el postest de 4,48, finalmente, se puede observar que los mejores resultados en el postest se presentaron en el grupo experimental; confirmando que el método aplicado mejora significativamente en la dimensión cambio. Se puede decidir que, al ser p < 0,05: nos permite aceptar la hipótesis de investigación y rechazar la hipótesis nula.
Cálculo de la prueba de hipótesis para evaluar diferencia de medias del pre y postest del grupo control y experimental para la dimensión comparación.
De acuerdo con los estadísticos analizados y tomando en cuenta la regla de decisión, se concluye que existe diferencia significativa en la dimensión comparación de la resolución de problemas matemáticos en estudiantes de segundo grado de una institución educativa de Trujillo, después de haber aplicado el Método Singapur, pues se tiene un valor de p<0,05, aceptándose la hipótesis alterna de desigualdad de medias. Al evaluar los promedios podemos identificar que en el pretest se tiene una nota promedio de 3,09 y en el postest de 4,90, finalmente, se puede observar que los mejores resultados en el postest se presentaron en el grupo experimental; confirmando que el método aplicado mejora significativamente en la dimensión comparación. Se puede decidir que, al ser p <0,05: nos permite aceptar la hipótesis de investigación y rechazar la hipótesis nula.
Cálculo de la prueba de hipótesis para evaluar diferencia de medias del pre y postest del grupo control y experimental para la dimensión igualación.
De acuerdo con los estadísticos analizados y tomando en cuenta la regla de decisión, se concluye que existe diferencia significativa en la dimensión igualación de la resolución de problemas matemáticos en estudiantes de segundo grado de una institución educativa de Trujillo, después de haber aplicado el Método Singapur, pues se tiene un valor de p<0,05, aceptándose la hipótesis alterna de desigualdad de medias. Al evaluar los promedios, podemos identificar que en el pretest se tiene una nota promedio de 1,66 y en el postest de 4,90, lo que significa que hubo un desempeño notablemente superior en el grupo experimental durante el postest, confirmando así que el método implementado logró mejorar significativamente la capacidad de los estudiantes. Se puede decidir que, al ser 𝑝< 0,05: nos permite aceptar la hipótesis de investigación y rechazar la hipótesis nula.
Prueba de comparaciones múltiples entre dimensiones de la variable resolución de problemas
Según el nivel de significancia del ANOVA es sig. = 0,000 siendo menor al 5% (p < 0,05), ello demuestra que la regresión es altamente significativa. Esto implica que el Método Singapur tiene un efecto significativo en la resolución de problemas matemáticos de los estudiantes.
Los resultados muestran una suma de cuadrados de regresión de 4007,494, un residuo de 9625,077, y una suma total de 13632,571, lo que indica que el método explica el 29,4% de la variabilidad total en el desempeño matemático de los estudiantes. La media cuadrática de regresión de 4007,494 y del residuo de 240,62, con grados de libertad de 1 y 20 respectivamente, confirman la robustez del modelo. Si bien estos datos validan estadísticamente la efectividad del Método Singapur como estrategia pedagógica, el residuo considerable sugiere la existencia de otros factores influyentes en el rendimiento matemático que no fueron considerados en el modelo. Estos resultados respaldan la implementación del método como una herramienta valiosa dentro de un enfoque educativo integral.
Análisis de regresión
De acuerdo con el análisis de regresión lineal confirma que la implementación del Método Singapur tiene un impacto positivo y significativo en la resolución de problemas matemáticos. Por cada unidad incrementada en la aplicación del método, se observa un aumento de 0,9 unidades en el rendimiento matemático (t = 4,08, p < 0,000), con un error estándar de 0,2. El modelo establece una constante de 26,8 (t = 4,403, p < 0.000) como nivel base, con un error estándar de 6,0. Los intervalos de confianza del 95% tanto para el coeficiente de regresión (0,4 a 1,3) como para la constante (14,5 a 39,1) confirman la solidez estadística del impacto positivo del método en el desempeño matemático de los estudiantes, validando su efectividad como estrategia pedagógica.
Prueba de comunalidades
Según la tabla 4, el análisis de las comunalidades mediante componentes principales muestra que las dimensiones de Comparación D3 (61%) e igualación D4 (64%) son las más representadas en el modelo, indicando que el programa de Método Singapur impactó significativamente en la resolución de problemas de este tipo. Esto significa, en términos generales, que estas dimensiones están relativamente bien presentes en el modelo. Las dimensiones Cambio D2 y Combinación D1 tienen comunalidades extraídas más bajas de (37%) y (35%) respectivamente. Esto significa que ambas dimensiones tuvieron una integración más débil en el modelo o aspectos únicos no capturados por los componentes principales. Estos resultados reflejan que la aplicación del programa de Método Singapur influyó más en los problemas relacionados con la comparación e igualación de cantidades, mientras que la combinación y cambio podrían requerir un enfoque más específico en futuros ajustes del programa.
Tabla 4.
Tabla de comunalidades.
|
Comunalidades |
Inicial |
Extracción |
|
D4: Igualación |
1,000 |
,647 |
|
D3: Comparación |
1,000 |
,619 |
|
D2: Cambio |
1,000 |
,373 |
|
D1: Combinación |
1,000 |
,359 |
Elaboración: Los autores.
Por último, según la tabla 5, el análisis factorial mediante componentes principales reveló una estructura tetradimensional que captura el 68,42% de la varianza total del fenómeno estudiado. La distribución de la varianza explicada presenta un patrón decreciente pero equilibrado entre los componentes principales (24,92%, 17.03%, 13,46% y 13,004% respectivamente). La rotación factorial optimiza esta estructura, redistribuyendo la varianza de manera más homogénea (20,37%, 18,03%, 16,60% y 13,41%), lo que sugiere una mayor estabilidad e interpretabilidad de los constructos subyacentes. Los componentes adicionales, con autovalores inferiores a la unidad, fueron excluidos según el criterio de Kaiser, aunque el quinto componente (autovalor=0,96) se aproxima al umbral de relevancia, sugiriendo una potencial complejidad adicional en la estructura factorial que podría ser considerada en análisis posterior.